Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Cauchy-Schwarz
#1 05. 04. 2016 11:01 — Editoval vanok (14. 06. 2016 07:35)
Cauchy-Schwarz
Pozdravujem,
V tomto vlakne http://forum.matweb.cz/viewtopic.ph … 89#p511989 sa hovori o dokaze nerovnosti Cauchy-Schwarz.
Ake dokazy tejto nerovnosti poznate?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 05. 04. 2016 12:34
Re: Cauchy-Schwarz
Pripomenme, ze prehilbertovskom priestore E, citovana nerovnost sa pise.
Pre  nenulove, mame
nenulove, mame
 .
.
Rovnost plati len a len ak 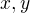 su linearne zavisle.
su linearne zavisle.
Kazdy dokaze prepisat, do vseobecnej formy, najznamejsi dokaz, ktory v citovanom prispevku nam pripomenul kolega Freedy.( asi vsetkych nas to tak ucili)
Iny dokaz ( a iste od teraz ho budete pouzivat) je zalozeny na zapise do rozvoja 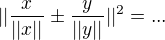 .
.
Ze to dokazete dokoncit.
Ine dokazy, ak poznate nejaky iny, tak rad sa poucim.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 25. 05. 2016 12:36
Re: Cauchy-Schwarz
Dalsia myslienka, ktora moze byt uzitocna na ine dokazy nerovnosti Cauchy-Schwarz.(NCS)
Predpokladajme ze sme v prehilbertovskom priestore (= euklidovsky priestor) E.
Je jasne, ze NCS pre urcite x,y v E, plati pochopitelne v jednom podpriestore dimenzie 2.
Cize aj, ak ju vieme dokazat v lubovolnom podpriestore dim 2, tak plati v celom priestore.
(Pochopitelne vsetki zname dokazy platia aj v podpriestoroch dim 2)
Neda va to inspiracie na nejaky iny dokaz?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 11. 06. 2016 17:54 — Editoval vanok (14. 06. 2016 06:07)
Re: Cauchy-Schwarz
Tu vyuzijem predosly prispevok ↑ vanok:.
Cize predpokladam, ze som v euklidovskom priestore s jednou ortonormalnou bazou.( ze taka baza existuje to iste kazdy vie v takomto priestore ukazat).
Nech x,y maju suradnice v tejto baze (a ,b) a (c,d)
Pre komplexne cisla  plati, ze realna cast sucinu
plati, ze realna cast sucinu 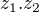 je skalarny sucin
je skalarny sucin  a jeho imaginarna cast je
a jeho imaginarna cast je 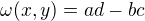 .
.
Vyraz 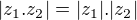 na druhu da
na druhu da
....
Staci ?
Ze to sami ukoncite.
Dobra novinka: podobny dokaz sa da generalizovat aj na hermitovsky sucin. (V jednom z nich sa pouziju kvaterniony )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 14. 06. 2016 07:06 — Editoval vanok (14. 06. 2016 07:21)
Re: Cauchy-Schwarz
Iste ste tiez rozmyslali co da 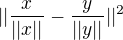 v pripade, ak uvazujeme hermitovsky skalarny sucin.
v pripade, ak uvazujeme hermitovsky skalarny sucin.
Urcite dokazete nerovnost:
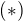
( ako mi to napisal aj kolega Freedy v pm, ale 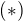 , nam da NCS vdaka malej uvahe)
, nam da NCS vdaka malej uvahe)
Pochopitelne to da rovnost len a len ak 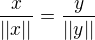 ( povedane slovamy: x,y su pozivne kolinearne)
( povedane slovamy: x,y su pozivne kolinearne)
Je celkom jednoduche ukazat, ze existuje komplexne cislo  take ze
take ze  a
a 
( staci zobrat  ak
ak  , inac polozme
, inac polozme 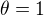 ).
).
A teraz ak pouzijeme vhodne vektory v 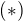 dostaneme NCS.....
dostaneme NCS.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 24. 06. 2016 11:32
Re: Cauchy-Schwarz
Doplnim tu vsetki podrobnosti dokazu, ( ako si to zela viacej kolegov)
Mame 
Nerovnost 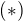 pre
pre  , da
, da 
( rovnost v pripade pozitivnej kolinearity)
Ak treba, mozem pridat aj definiciu hermitovskeho skalarneho sucinu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Cauchy-Schwarz
