Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 07. 2016 12:55
Zaujimava postupnost
Poculi ste o tejto postupnosti ?
?
Popiste jednoducho ako je vytvorena.
Ako vyjadrit jej n-ty clen?
Je periodicka?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 08. 07. 2016 23:29
Re: Zaujimava postupnost
Ta postupnost ma zaujimave vlasnosti....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 09. 07. 2016 10:30
Re: Zaujimava postupnost
Zdravím,
nikdy jsem o ní nepočul.
Ale Google poradil: Kolakoski sequence
Co je na ní zajímavého? Tedy pro mě? Že ze zvyšující délkou sekvence se poměr jedniček a dvojek se blíží jedné. A že nikdy po sobě nenásledují tři nebo více stejných čísel. Periodická asi nebude. Na co se to hodí - netuším.
Offline
#4 09. 07. 2016 11:13
Re: Zaujimava postupnost
↑ mák:,
Ahoj,
Napriklad urcitym sposobom sa popisuje sama.
Mas
1nu 1
2 ......2
2 .....1
1....1
1....2
atd.
Inac povedane, postupne dlzka kazdeho bloku jedniciek, dvojek nam da danu postupnost.
Vdaka tejto vlasnosti mozes uplne konstruhovat danu postupnost. Skus.
Uz to je zaujimave.
Vidim, ze google ti aspon pomohol najst meno tejto postupnosti.
Na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 09. 07. 2016 11:59 — Editoval mák (09. 07. 2016 12:02)
Re: Zaujimava postupnost
No včera jsem se s tím zabýval, ale myslím, že takhle jednoduše to nejde popsat. Zjistil jsem, že nejsem schopen zjistit následující číslo bez toho, aniž bych věděl součet všech předcházejících čísel v sekvenci. Takže výsledný program vypadá takto:
Code:
Kolakoski_sequence(n):=block([a,kn:0,i,k,Q],
a: makelist(0,i,1,max(4,2*(n))),
[a[1],a[2],a[3]]: [1,2,2],
for k:1 thru n step 2 do (
kn: kn + a[k],
a[kn]: 1,
a[kn+1]: 2,
kn: kn + a[k+1],
a[kn+1]: 1,
a[kn]: 2
),
Q: delete(0,a),
Q
);Je tam vidět suma všech čísel 
Bez tohoto by byla sekvence periodická, takto vypadá, že není.
Možná, by to šlo napsat jednodušeji, tedy myslím, bez znalosti předcházejících členů, ale nepřišel jsem na to.
Offline
#6 09. 07. 2016 12:29 — Editoval vanok (09. 07. 2016 12:44)
Re: Zaujimava postupnost
Tak sa pokus il to popisat.
Popis postupnosti co ma vlasnost co som popisal a zacina s 1
Dalsi clen nemoze byt 1, to by bol spor. Tak postupnost zacina takto 1,2,? Co znamena vdaka jej popisu ze mame 1,2,2,?
? musi byt 1 staci?
Ak by si to chcel lepsie popisat, mozes danu postupnost oznacit 
A postupnost co popisuje  . ( zaroven
. ( zaroven  ...)
...)
Tvoj predosly prispevok musim este v klude pozriet.
Mas moznost vyskusat tvoj kod?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 09. 07. 2016 13:57
Re: Zaujimava postupnost
Můj kód určitě funguje, a generovaná sekvence souhlasí (kontroloval jsem prvních 10000 členů podle b000002.txt.
Offline
#8 09. 07. 2016 14:02
#9 09. 07. 2016 15:32
Re: Zaujimava postupnost
Vyborne,
Teraz sa pokusme ukazat, ze tato postupnost nie je periodicka.
To sa da vyjadrit aj takto: cislo 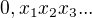 kde
kde 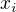 su cleny danej postupnosti je iracionalne.
su cleny danej postupnosti je iracionalne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 09. 07. 2016 18:41
Re: Zaujimava postupnost
No to umím pouze hrubou silou.
Hledám opakující se sekvence:
Například sekvenci prvních 66 až 99 čísel najdu až na pozici 23374. A čím delší číslo hledám, tím dále je.
Další sekvence prvních 100 až 150 čísel je nalezená až na pozici 35981.
Sekvence prvních 151 až 226 čísel je nalezená až na pozici 53975.
Sekvence prvních 227 čísel je nalezená až na pozici 80982.
To by mohl být důkaz?
Offline
#11 09. 07. 2016 18:44
Re: Zaujimava postupnost
↑ mák:,
Dnes nemam uz cas. Zajtra dam jeden mozny dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 10. 07. 2016 17:31
Re: Zaujimava postupnost
mák napsal(a):
...
Sekvence prvních 151 až 226 čísel je nalezená až na pozici 53975.
Sekvence prvních 227 čísel je nalezená až na pozici 80982.
To by mohl být důkaz?
Musim povedat, ze na cloveka s tak dobrymi programatorskymi schopnostami ma tvoja predstva o dokaze dost prekvapuje. To, co pises, je ekvivalentne nasledujucemu dialogu:
A: Vsetky prirodzene cisla su mensie ako  . Dokazte.
. Dokazte.
B: Skusil som to pre cisla od 1 az po  a je to tak ... To by mohol byt dokaz?
a je to tak ... To by mohol byt dokaz?
Offline
#13 10. 07. 2016 19:28 — Editoval Marian (10. 07. 2016 20:39)
Re: Zaujimava postupnost
↑ vanok:
O problémech tohoto typu si myslím své (a nic pozitivního to není - i zde na fóru). Ale pokud se odosobním od své silné averze k úlohám typu "Doplňte posloupnost prvků {1,2,3,4,5,?}.", tak potom postrádám definici studované posloupnosti. Je možné, že jsem něco (=exaktní definici) přehlédnul. A původní příspěvek skutečně nic přesnějšího o popisu nepřináší (možná je to záměr).
Pokládám si otázku: "Jak mám dokazovat vlastnosti něčeho, co je dáno tak vágně?" Ačkoliv jsem si přečetl další příspěvky, považuji je za spekulativní (EDIT: kromě #12). Posloupnost prvních několika členů vůbec nevypovídá o vlastnostech nekonečné posloupnosti. Zbytek členů uvedené posloupnosti si totiž mohu vymyslet tak, jak zrovna bude vát vítr.
Omluvte můj ortodoxní přístup, ale domnívám se, že toto fórum je věnováno matematice a nikoliv výtvarné výchově, kde si mohu obrázek dokreslit tak, jak mě v noci políbí můza.
Offline
#16 10. 07. 2016 20:48
Re: Zaujimava postupnost
↑ Marian:,
No tak vyraz "jednoduchy popis postupnosti" povazuj za jedno mozne riesenie.
Iste by sa dala zlepsit a zdokonalit dana otazka #1.
Zda sa mi, ze aj najlepsie texty sa mozu zdokonalit.
Tak, kludne mozes dat inu verziu danej otazky.
Ty si skutocne taky clovek co pise len dokonale texty?
Ak je to tak, tak mi ostava ti len gratulovat.
P.S. Je lepsie vidiet veci z pozitivneho hladiska, ako nieco, ci niekoho systematicky kritizovat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 10. 07. 2016 23:23
Re: Zaujimava postupnost
↑ vanok:pozri si Marianove príspevky na fóre nejde o negativizmus ale o to že na pôvodnú otázku nie je možné jednoznačne odpovedať resp. odpoveď je že hľadaná postupnosť má prvých niekoľko členov určených výpisom a ďalšie sú určené nejakou postupnosťou prirodzených čísel . Keď máme totiž ľubovoľný konečný zoznam čísel (prirodzených či hocijakých to je jedno) tak existuje k nemu nekonečne veľa postupnosťí ktoré ním začínajú nekonečne veľa ich je periodických ( dokonca pre každé prirodzené číslo nie menšie ako dĺžka zoznamu existuje nekonečne veľa postupností s periódou tej dĺžky ) a nekonečne veľa je neperiodických.
MATH IS THE BEST!!!
Offline
#18 11. 07. 2016 00:36
Re: Zaujimava postupnost
↑ jarrro:,
Kolega dobre pochopil co som napisal.
Jedno jednoduche riesenie je to co som pripomenul.
Tak sa mozme o to riesenie zaujimat.
Kazdy clovek, ja, ty, on moze napisat nedokonaly text. Ale to neznamena ze ho treba odhodit.
Tak sa mozes zaujimat o tu postupnost vdaka #4.
A to som jasne uz vyssie napisal.
Aj Euler napisal 1+2+3+4+5+6+7+… = -1/12, no vsak ak sa nezastavis na tom zapise mozes najst mozno nieco zaujimave.
P.S. To iste ako v #16
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 11. 07. 2016 06:12 — Editoval Marian (10. 10. 2016 06:46)
Re: Zaujimava postupnost
↑ vanok:
Obával jsem se takové reakce a ve skrytu duše očekával jinou. Nestalo se - bohužel.
Ale jak vysvětluje jarrro, ze tvého původního zadání, tj.
vanok napsal(a):
Poculi ste o tejto postupnosti
Popiste jednoducho ako je vytvorena.
Ako vyjadrit jej n-ty clen?
Je periodicka?
není možné jednoznačně určit vlastnosti nebo posloupnost seriózně studovat. Je jisté, že asi každý text je možné vylepšit. Nikde jsem nenapsal, že je tvůj text nutno odhodit, případně, že je nepoužitelný. Dával jsem si dobrý pozor na to, co jsem psal. Taktéž netvrdím, že mé příspěvky nebo texty jsou dokonalé. Znám se velmi dobře na to, abych objektivně a veřejně vyjádřil své politování nad tím, kolik chyb jsem schopen udělat v matematickém textu.
Můj původní záměr v #13 byl jiný, totiž poukázat na fakt, že je otázka položena nesprávně. Oceňuji, že mi dáváš možnost to vylepšit. Ale to ještě neznamená, že vím, jak otázku nebo problém položit jednoznačně. Já to nevím, aniž bych nezatajil některé význačné vlastnosti takto zvláštní posloupnosti, proto bych ji nepokládal. Taktéž nevím, proč přesně má třeba ↑ Andrejka3: tyto úlohy ráda (škoda, že myšlenku nerozvinula). V jistém didaktickém smyslu mohou doplňovací úlohy rozvíjet matematické myšlení. Ovšem pouze do doby, kdy bude nějaký žák protestovat, že našel své pravidlo pro tvoření dalších členů neúplné posloupnosti, které může být srovnatelně smysluplné jako zamýšlené tvoření, které zná pedagog. Tady je nutno hodnotit zvláště opatrně a individuálně - to je však ovlivněno subjektivismem pedagoga - nezpochybnitelná nevýhoda.
Není také pravda, že můj příspěvek je dílem systematické kritiky. Mám špatnou paměť, ale kolegu vanka jsem mimo toto vlákno kritizoval ještě za přidání concluding remarks s odkazem na řešení jako úvodní příspěvek k mnou zadanému problému v sekci zajímavých úloh, což se evidentně nehodí. Spíše než o systematické kritice bych proto hovořil o konstruktivní kritice, stejně jako i v tomto vláknu.
Odcituji ještě jiné místo: "Kolega dobre pochopil co som napisal." Obdivuji tvou jistotu, ale skutečně jsem nepochopil, o co se v zadání jedná (proto jsem se ozval). Důvody popsal jarrro a naznačil v tomto příspěvku i já. Toto místo mě mrzí nejvíce. Nemůžeš se veřejně vyjadřovat za někoho jiného a říkat, že něco dobře pochopil. (The respect, the politeness are essential qualities.)
Co se Eulera týče, viz "Aj Euler napisal 1+2+3+4+5+6+7+… = -1/12, no vsak ak sa nezastavis na tom zapise mozes najst mozno nieco zaujimave.", matematický formalismus jeho a naší doby je nesrovnatelný. Dokonce i formalismus později v době Riemanna je ještě místy značně nejistý (viz třeba jeho známé práce, které souhrnně vyšly i v moderní době při zachování původního formalismu) - prolistujte si je.
Na závěr bych rád připomenul, že komunita matematiků musí být k sobě rozumně přísná - to je přeci podstatou peer review procesů a nakonec i toho, že se jedná o královnu věd.
Offline
#20 11. 07. 2016 10:18 — Editoval vanok (11. 07. 2016 11:39)
Re: Zaujimava postupnost
↑ Marian:,,
Tak som sa zmylil, mal som napisat, ten prispevok #4 mozno nepochopil. ( Prepac, skutocne sa ti omluvam ). Asi sa casom zlepsim.
Co som ti napisal, v #16, ze mozme studovat jedno mozne riesenie. ... Preco nie?
Zda sa ze Kolakoski dal tu istu otazku ako #1 a zda sa ze to urobil v casopise MAA.( niekedy v druhej polovici 20 teho storocia) ... Viaceri ludia to pochopili ako prvy priklad postupnosti "co sa cita sama"...
Otazka doplnit nejaku postunost a otazka hladat mozne vlasnosti nejakej postupnosti, nie su, aspon si myslim, ulohy toho isteto typu.
Co sa tyka, nedorozumenia, ze som pridal historicky doplnok z webu na tvoju zaujimaju ulohu, neviem preco to sa ti to nepacilo.. Vsak to pekne doplnilo tvoj prispevok.
P.S.
PS2. Mohli y sme sa vratit k danej postupnosti. A skusit ukazat, ze ak postupnost dana v #1 je urcena ( neformalne povedane) ako v #4, tak nemoze byt periodicka.
Édit. Oprava pravopisu mena Kolakoski a nie Kolakovski
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 11. 07. 2016 15:32
Re: Zaujimava postupnost
Dakujem Marianovi za velmi rozumne komentare k pojmu postupnost. Som tiez odporcom uloh "doplnte dalsi clen postupnosti", navyse dodam, ze nie raz sa mi stalo, ze student pri pokuse o definiciu postupnosti trval na tom, ze medzi prvkami postupnosti musi byt akasi zakonitost.
Offline
#22 11. 07. 2016 16:05 — Editoval vanok (12. 07. 2016 22:29)
Re: Zaujimava postupnost
Drahi kolegovia, akoze ze ste vyjadrili vas nazor, ktory respektujem a tak pokracujem z tym o co ide v tomto vlakne. Ak si myslite ze treba pokracovat v diskuziu o spatne polozenych otazkach mozte kludne otvorit nove vlakno na taku temu.
Dokaz ze dana postupnost ktorej prvy clen je 1( Cf. #1, #4) nie je periodicka, a to ani len od urciteho indexu n. ( cize jej cleny pouzite postupne v cisle  nedaju rationalne cislo, ale daju iracionalne cislo).
nedaju rationalne cislo, ale daju iracionalne cislo). 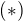
Pozor, ide neformalny dokaz, kto chce moze si ho kludne formalizovat.
Najprv upresnim niekolko pojmov, aby tu nezacali zasa nejake neplodne diskusie.
Kazda pripadna nekonecna postupnost, v nasledujucom dokaze, bude typu, 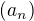 kde n je nenulove cislo ktore
kde n je nenulove cislo ktore  , a
, a  cele cislo, a na viac, ak to bude uzitocne tak na jej oznacenie pouzijem zapis
cele cislo, a na viac, ak to bude uzitocne tak na jej oznacenie pouzijem zapis 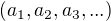 .
.
( toto oznacenie, preto aby kazdy jej clen bol dobre urceny).
Povedat, ze celociselna postupnost  ma popisosovu postupnost
ma popisosovu postupnost  , znamena, ze popisova postupnost ma za jej cleny dlzky blokov, ktore su vytvorene po sebe nasledujucimi rovnakymi clenmy postupnosti
, znamena, ze popisova postupnost ma za jej cleny dlzky blokov, ktore su vytvorene po sebe nasledujucimi rovnakymi clenmy postupnosti 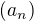 ( pochopitelne dva nasledujuce bloky su vytvorene inymi cislami).
( pochopitelne dva nasledujuce bloky su vytvorene inymi cislami).
Na priklad, ak  zacina takto,
zacina takto, 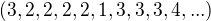 , tak popisova postupnost
, tak popisova postupnost  zacina takto
zacina takto  .( v priklade pouzita postupnost nie je taka ako tu ktoru budem podrobne vysetrovat, tato je pouzita len na ilustraciu vseobecneho pojmu "podpisova postunnost" lubovolnej postupnosti)
.( v priklade pouzita postupnost nie je taka ako tu ktoru budem podrobne vysetrovat, tato je pouzita len na ilustraciu vseobecneho pojmu "podpisova postunnost" lubovolnej postupnosti)
V pripade postupnosti co studujem, je jasne, ze  a tiez, ze
a tiez, ze  tak od teraz to budem predpokladat.
tak od teraz to budem predpokladat.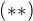
( je tiez jasne, ze kazdy blok tejto postupnosti moze mat vylucne dlzku 1 alebo 2).
Dokaz vlasnosti 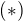 urobim sporom.
urobim sporom.
Preto predpokladam, ze existuje prirodzene nenulove cislo  jedna perioda
jedna perioda  ( ktoru vyberiem najmensiu moznu): co znamena, ze
( ktoru vyberiem najmensiu moznu): co znamena, ze 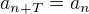 pre kazde prirodzene
pre kazde prirodzene 
Nech  ( respektivne
( respektivne  ) je pocet indexov
) je pocet indexov  , takych, ze
, takych, ze  takych, ze
takych, ze  ( resp.
( resp.  ).
).
Tak 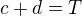
Vdaka 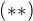 ,
,  je tiez jedna ina perioda postupnosti, a tak musi byt nasobok najmensej periody
je tiez jedna ina perioda postupnosti, a tak musi byt nasobok najmensej periody  , a tiez plati
, a tiez plati  .
.
Ale to je nemozne. ( Co je hladany spor.)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 11. 07. 2016 16:42 — Editoval jarrro (11. 07. 2016 16:43)
Re: Zaujimava postupnost
↑ vlado_bb:akasi určite . aj elementárnymi a analytickými nástrojmi(nekonečný rad, integrál, inverzná funkcia apod.)nepopísateľná funkcia je zákonitosť
MATH IS THE BEST!!!
Offline
#25 12. 07. 2016 12:31
Re: Zaujimava postupnost
Drahi kolegovia ↑ vlado_bb:↑ jarrro:,
Ak si myslite, ze treba pokracovat vasu diskuziu, tak prosim otvorte na to ine vlakno. Dakujem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


