Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti prvočísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 08. 2016 21:56
Vlastnosti prvočísel
Ahoj mám k dispozici následující dvě věty:
1. Prvočíslo 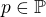 se nachází v rozkladu n! právě
se nachází v rozkladu n! právě ![kopírovat do textarea $\sum_{k \ge1 }^{}[\frac{n}{p^k}]$](/mathtex/a2/a2efa54fa8b93001efe4133e97f788bb.gif) krát. (
krát. (![kopírovat do textarea $[]$](/mathtex/3a/3ab885809b900a748009c66b5ce5e3cb.gif) značí celou dolní část)
značí celou dolní část)
2. Prvočíslo 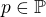 se nachází v rozkladu kombinačního čísla
se nachází v rozkladu kombinačního čísla  právě
právě ![kopírovat do textarea $\sum_{k \ge1 }^{}([\frac{2n}{p^k}]-2[\frac{n}{p^k}])$](/mathtex/2a/2ab21e35bacedb12a4bd6914ddd1d50f.gif) krát, tj. nanejvýš r-krát, kde
krát, tj. nanejvýš r-krát, kde 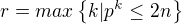
a z nich mám odvodit následující:
1. pokud pro 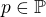 platí
platí  , pak se p v rozkladu
, pak se p v rozkladu  nevyskytuje
nevyskytuje
2. pokud pro 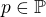 platí
platí  , pak p se v rozkladu
, pak p se v rozkladu  nachází nanejvýš jednou
nachází nanejvýš jednou
budu rád za každou radu
Offline
- (téma jako vyřešené označil(a) Hertas)
#2 04. 08. 2016 18:21
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vlastnosti prvočísel
Ahoj, co třeba druhý bod 1. Zkus si rozepsat čitatele a jmenovatele toho kombinačního čísla.
"Máte úhel beta." "No to nemám."
Offline
#3 08. 08. 2016 20:45
Re: Vlastnosti prvočísel
číslo  odhadnu číslem
odhadnu číslem 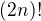 a potom podle první věty a předpokladu, že
a potom podle první věty a předpokladu, že  stačí vzít nejmenší takové číslo (prvočíslo je speciální případ přirozeného čsla, takže to musí fungovat), tj.
stačí vzít nejmenší takové číslo (prvočíslo je speciální případ přirozeného čsla, takže to musí fungovat), tj. ![kopírovat do textarea $p=[\sqrt{2n}] + 1$](/mathtex/4e/4ebe7efb694b6e00c018db88b771e381.gif) a po dosazení dostaneme:
a po dosazení dostaneme:![kopírovat do textarea $\sum_{k \ge1 }^{}[\frac{2n}{([\sqrt{2n}]+1)^k}]$](/mathtex/19/19765f5eb4c09280d1b9e1beb9ac4ed2.gif) , takže se v rozkladu nachází opravdu nanejvýš jednou
, takže se v rozkladu nachází opravdu nanejvýš jednou
a nevěděl bys mě nakopnout s tím prvním bodem?
Offline
#4 08. 08. 2016 22:39
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vlastnosti prvočísel
↑ Hertas:
Ahoj, nerozumím tomu prvnímu odhadu - čeho tím odhadem docílíš?
"Máte úhel beta." "No to nemám."
Offline
#6 09. 08. 2016 16:26
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vlastnosti prvočísel
↑ Hertas:
Jenže to ti nic neřekne o tom čísle  .
.
"Máte úhel beta." "No to nemám."
Offline
#9 09. 08. 2016 21:39
Re: Vlastnosti prvočísel
ani ne :)
už to tam vidím, největší prvočíslo, jež se v rozkladu celého čísla  nachází, je
nachází, je 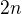 (což pro n > 1 není prvočíslo), tím pádem prvočíslo
(což pro n > 1 není prvočíslo), tím pádem prvočíslo  se v jeho rozkladu může nacházet nanejvýš jednou
se v jeho rozkladu může nacházet nanejvýš jednou
Offline
#10 11. 08. 2016 00:48
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vlastnosti prvočísel
↑ Hertas:
Já zkoumám ale bod 1, i když asi to bude podobné. Musíš si říct kolikrát je to p v čitateli a kolikrát ve jmenovateli...
"Máte úhel beta." "No to nemám."
Offline
#11 11. 08. 2016 11:44 — Editoval Brano (30. 08. 2016 10:26)
Re: Vlastnosti prvočísel
bod 1)
Pre 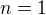 tvrdenie plati trivialne, lebo nieje ziadne prvocislo v intervale
tvrdenie plati trivialne, lebo nieje ziadne prvocislo v intervale ![kopírovat do textarea $(2n/3,n]$](/mathtex/51/51f0dbdf4a2c69d654c68c09387f43af.gif) .
.
Pre 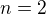 tvrdenie neplati, lebo
tvrdenie neplati, lebo 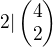 .
.
Pre  mame v danom intervale jedine prvocislo
mame v danom intervale jedine prvocislo 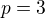 a lahko overime, ze prislusne kombinacne cisla nedeli.
a lahko overime, ze prislusne kombinacne cisla nedeli.
Pre 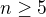 plati
plati  a teda pre
a teda pre  plati
plati  a teda
a teda![kopírovat do textarea $\left[\frac{2n}{p^k}\right]=\left[\frac{n}{p^k}\right]=0$](/mathtex/58/58a3747c86cbfa33e893b81ac1814d9f.gif) . A kedze
. A kedze  tak
tak  a
a  , cize
, cize ![kopírovat do textarea $\left[\frac{2n}{p}\right]=2\left[\frac{n}{p}\right]=2$](/mathtex/b0/b0c036a1d977509fa74477111199a141.gif) . Z druhej vety dostaneme, ze
. Z druhej vety dostaneme, ze  sa v
sa v 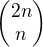 nachadza
nachadza 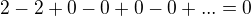 krat, teda sa tam nenachadza.
krat, teda sa tam nenachadza.
bod 2)
pre  plati
plati  a teda
a teda ![kopírovat do textarea $\left[\frac{2n}{p^k}\right]=\left[\frac{n}{p^k}\right]=0$](/mathtex/58/58a3747c86cbfa33e893b81ac1814d9f.gif) . Dalej mozme napisat
. Dalej mozme napisat  kde
kde  a teda
a teda 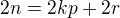 a teda plati
a teda plati ![kopírovat do textarea $\left[\frac{n}{p}\right]=k$](/mathtex/e4/e4d863d74b2d87a564dcdbe6d1739d99.gif) a
a ![kopírovat do textarea $\left[\frac{2n}{p}\right]=2k+\left[\frac{2r}{p}\right]$](/mathtex/1a/1a87950718f82f000f856bc8e3d7bdd5.gif) . Dostaneme teda, ze
. Dostaneme teda, ze  sa v
sa v 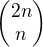 nachadza
nachadza ![kopírovat do textarea $2k+\left[\frac{2r}{p}\right]-2k = \left[\frac{2r}{p}\right]$](/mathtex/f3/f3ac7016f63afb32a5aea5f553f6b339.gif) krat, co je bud
krat, co je bud  alebo
alebo  .
.
Offline
#12 11. 08. 2016 23:18 — Editoval vanok (12. 08. 2016 10:38)
Re: Vlastnosti prvočísel
poznamka.
Kolega ↑ byk7:, polozil velmi dobru otazku.
Pripominam, ze v knihe Proofs from the books, je dokaz Beltranoveho postulatu ktory vyuziva aj otazky z ↑ Hertas: ( ktore su tam aj dokazane).
Tiez moze byt poucne precitat
http://www.cut-the-knot.org/arithmetic/ … late.shtml
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 12. 08. 2016 22:53
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Vlastnosti prvočísel
Ad 1) Takové p se v tom kombinačním čísel vyskytuje v čitateli i jmenovateli právě 2x a tedy se vykrátí...
"Máte úhel beta." "No to nemám."
Offline
#14 13. 08. 2016 00:17
Re: Vlastnosti prvočísel
Ahoj ↑ check_drummer:
Maly doplnok......
Podrobnejsie, pretoze 
da  .
.
Co znamena, ze  nie je depitelne prvocislom p...... Atd.....
nie je depitelne prvocislom p...... Atd.....
Ale v odkaze co som napisal vcera, je to uz dokazane ( I ked bez podrobnosti)... Dobru noc.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti prvočísel (TOTO TÉMA JE VYŘEŠENÉ)
