Matematické Fórum

↑ malarad:

Není. Kubická parabola nemá ani ohnisko, ani řídicí přímku.

↑ malarad:

Sám píšeš kubická "parabola".

Prečítaj si definíciu paraboly.

↑ malarad:

No - to nie je definícia paraboly.

Definícia:  Parabola je množina všetkých bodov v rovine E2, ktoré majú rovnaké vzdialenosti od danej priamky d a od daného bodu F, pričom F  nepatrí d.

(3) Symbolický zápis: parabola = {X patriacichb E2; |Xd| = |XF|, F nepatrí d}


F – ohnisko
d – riadiaca priamka
p – parameter paraboly: p = |Fd|
o – os: F patrí  o,  o je kolmá na d
V – vrchol: V patrí o a platí |Vd| = |VF|

To, čo píšeš, sú niektoré vlastnosti paraboly, nie jej definícia.

Kde presne je ohnisko tvojej paraboly? A jej riadiaca priamka?

Dôsledok definície paraboly je totiž rovnica paraboly, ktorá nie je  .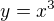

Kubická parabola má úplne inú definíciu. Žiadne ohnisko, žiadna riadiaca priamka.