Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet neurčitého integrálu pomocí substituce (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 09. 2016 20:05
- dominiksep
- Příspěvky: 54
- Reputace: 0
Výpočet neurčitého integrálu pomocí substituce
Ahoj, trošičku jsem se pral s vysvětlením výpočtu neurčitého integrálu pomocí substituce (v tý učebnici by to mohli líp rozepsat) a s něčím bych potřeboval poradit.
U první substituční metody bych potřeboval zjistit, jestli to chápu správně:
Nahrazuji funkci proměnnou. Využívám vztahu pro derivaci složené funkce:![kopírovat do textarea $\left [ G(\varphi (x) \right )]'=G'\left [ \varphi (x) \right ]\cdot \varphi' (x)=g\left [ \varphi (x) \right ]\cdot \varphi' (x)$](/mathtex/05/051d3ff26f64bf6e5203336daf61448f.gif) (1)
(1)
Z toho mi vyjde:![kopírovat do textarea $\int g\left [ \varphi (x) \right ]\cdot \varphi' (x)=G(\varphi (x))$](/mathtex/2b/2b8a69b68e254717f7c05a8ce3c269ca.gif)
Takže principiálně potřebuju najít nějaký 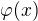 a k němu
a k němu  . Příklad:
. Příklad: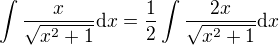
Tady jsem si to 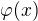 a
a  našel:
našel:
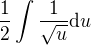
V předchozím kroku jsem se zbavil  , neboť podle vzorce (1) mi stejně nakonec "zmizí". Vysvětlil jsem si to dobře? Poté pokračuji následovně:
, neboť podle vzorce (1) mi stejně nakonec "zmizí". Vysvětlil jsem si to dobře? Poté pokračuji následovně: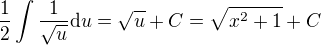
Je to správně?
A nyní druhá substituční metoda. Byl zde uveden příklad: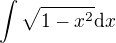

Tak tady už začínám mít trochu problém. Ja vůbec můžu nahradit x sinem? Jak z toho sinu vydoluji třeba hodnotu 10? V tomto případě to nevadí, protože definíční obor funkce odpovídá oboru hodnot sinu, ale to jsem si musel domyslet a kniha se o něčem takovým vůbec nezmiňuje...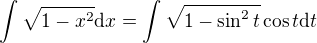
V tomto kroku mám problém s tím, že se tam najednou objevuje cos(t). Jak to tam můžu jen tak přidat? To si to můžu prostě jen tak vynásobit kosinem? Zbývající část příkladu už chápu.
Díky,
Dominik
Offline
- (téma jako vyřešené označil(a) dominiksep)
#2 16. 09. 2016 20:31 — Editoval misaH (16. 09. 2016 20:31)
- misaH
- Příspěvky: 13459
Re: Výpočet neurčitého integrálu pomocí substituce
↑ dominiksep:
Potrebuješ nahradiť nielen x, ale aj dx.
Ak miesto x dáš sint, tak 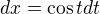 (derivácia)
(derivácia)
Offline
#3 16. 09. 2016 20:53
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Výpočet neurčitého integrálu pomocí substituce
↑ misaH:
OK, už mi začíná svítat. Můžete to někdo prosím obecně rozvést? O tomhle se v tý knize nezmiňují ani okrajově.
Offline
#5 17. 09. 2016 11:24 — Editoval dominiksep (17. 09. 2016 11:25)
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Výpočet neurčitého integrálu pomocí substituce
↑ jarrro:
Já jsem tu podmínku pochopil tak, že si v tom předpisu integrované funkce mám najít to g(x) i g'(x) jako jsem to udělal u té první metody.
Je to teda tak, že u té druhé si mám domyslet x=g(t)=sin(t) a abych získal to g'(t)=x'=1, tak mám udělat:
Ta jednička je hledaná derivace x. Pokud si tedy za x dám sin(t), bude derivace x (tedy jednička) cos(t).
Chápu to správně?
Díky
Dominik
Offline
#6 17. 09. 2016 12:04 — Editoval jarrro (17. 09. 2016 12:05)
Re: Výpočet neurčitého integrálu pomocí substituce
↑ dominiksep: áno niekedy je jednoduchšie priamo zintegrovať súčin 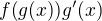 ( Napr. sa v ňom niečo pekne vykráti na tabuľkovú funkciu.)
( Napr. sa v ňom niečo pekne vykráti na tabuľkovú funkciu.)
A niekedy je tabuľková práve fcia f potom je účelnejšie intergrovať ( podľa t a na konci sa vrátiť) 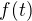
Inak je to stále iný prepis vety o derivácii zloženej fcie
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet neurčitého integrálu pomocí substituce (TOTO TÉMA JE VYŘEŠENÉ)

