Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Jak určit amplitudu a 0 funkce sinus?
#1 20. 09. 2016 11:14 — Editoval Berger (20. 09. 2016 11:30)
Jak určit amplitudu a 0 funkce sinus?

Mějme pole bodů o kterém víme, že jsou od sebe vzdáleny konstantní čas dt (například 100ns) a leží na sinusovce. O sinusovce víme jen její frekvenci, tzn. že její průchody 0 od sebe leží čas tp (například 5000 ns). Kde dané body na sínusovce leží nevíme .
Co chceme zjistit?
1. Amplitudu dané sínusovky, tedy y souřadnici nejvýše/nejníže položeného bodu
2. Čas průchodu 0 , tedy x souřadnici bodu, který má y=0
A to celé přesněji než například vzít kladný a záporný bod, který leží nejblíže 0, proložit jimi přímku a dopočítat bod v kterém ona protne osu x.
Offline
#4 09. 10. 2016 13:23
Re: Jak určit amplitudu a 0 funkce sinus?
Vrátím se k tématu.
Jak chcete prokládat sin když neznáte parametry funkce ?
Offset se dá korigovat .
Zatím to vidím takto:
Najdu dva body ležící nejblíže osy x, tak, aby jeden ležel nad a druhý pod osou
Pomocí rovnice přímky dopočítám souřadnici x bodu g který leží na přímce procházející body x1 a x2 a má souřadnic y=0.
Ten, ale není totožný s souřadnicí bodu ležící na sinusovce.,
Jediné na co jsme přišel, je možnost dopočítat chybu mezi těmito dvěma body.
Pokud se nepletu tak , by mělo patit
Error = | (sin(g) / sin (dt-g) - (x1/x2) |
Co na to říkáte?
Nejde to nějak elegantněji?
Offline
#5 09. 10. 2016 18:34
Re: Jak určit amplitudu a 0 funkce sinus?
Zdravím,
rovnice bude:
Přičemž A je hledaná amplituda a P je posun na souřadnici x, kde sinusovka protíná nulu.
Pokud budeš tedy znát dva body o souřadnicích [x1,y1] a [x2,y2] dosadíš a vyřešíš dvě rovnice.
Offline
#6 09. 10. 2016 23:36 — Editoval medvidek (09. 10. 2016 23:45)
Re: Jak určit amplitudu a 0 funkce sinus?
↑ mák:
Díky
↑ Berger:
Jen doplním, že místo vyjádření harmonických kmitů ve tvaru
je zde výhodné použít ekvivalentní zápis
Frekvenci (jak píšeš na začátku) známe, tudíž po dosazení dvou bodů (jak radí Mák) o souřadnicích [x1,y1] a [x2,y2] dostaneš dvě lineární rovnice, z nichž vypočteš  .
.
Tvoje vyjádření chyby asi nebude správné.
POZNÁMKA:
Téma je nesprávně umístěno v sekci VŠ pokročilá matematika. Pokud v něm budeme pokračovat, přesunu ho do sekce Ostatní ... dotazy pro praxi.
Offline
#7 10. 10. 2016 19:26
Re: Jak určit amplitudu a 0 funkce sinus?
Možná jsem natvrdlý, což je dnes docela možné, protože dnes asi nemám své dny a neměl bych se pouštět do žádných větších akci ,
ale tohle snad platí u volných harmonických kmitů jen pokud známe počáteční fázi kmitů. Jinak řečeno máme souřadnou soustavu položenou v nějakém z bodu kde je u sinu y=0.
To my ale nevíme, jinak řečeno známe souřadnice y obou bodu ,ale souřadnice x neznáme absolutně, ale jen relativně. Pokud tedy souřadná soustava leží v bodě x=0 y=0 tak mi o prvním bodě víme, že leží v x=t a druhý v x=t+10, aLE hodnotu t neznáme.
Offline
#8 10. 10. 2016 19:38
Re: Jak určit amplitudu a 0 funkce sinus?
Zdravím,
↑ medvidek:
tvůj zápis dává jednodušší rovnice, proto je lepší.
↑ Berger:
Souřadnice x nepotřebuješ znát absolutně, stačí relativně. Prostě některý označíš jako počátek.
Offline
#9 11. 10. 2016 00:25
Re: Jak určit amplitudu a 0 funkce sinus?
Ono není nad to to zkusit.
x1=1/10E6*10
y1=1,339566987
x2=x1+1/10E6
y2=1,469463131
Toto jsou dva body s absolutními souřadnicemi, které leží na ideální sinusovce o f=100kHz o amplitudě +- 2,5
Pro výše uvedené absolutní souřadnice můžeme řešení zde probíraných rovnic získat A1=2,4951 je tam sice relativně velká chyba, ale dejme tomu že vznikla nějakým zaokrouhlováním.
Protože absolutní souřadnice na ose x neznáme provedeme stejný výpočet po
x1=0, ostatní bude stejné.
Mě vyšlo A1=2,11
Což celkem odpovídá mému předpokladu, viz předešlý příspěvek,
Na vysvětlenou dva body jsou matematicky generované jako 10 a 11 vzorek na sinusovce s počátkem 0,0 , frekvence sinusovky 100kHz oversampling je 100 tj. 100 vzorků/perioda.
proto je souřadnice x1 1/10MHz*10vroek a x2 o 1/10MHz více.
Generovno v matlabu, stejně jaké následný výpočet. zd eprobianych rovnic.
Jelikož jsme to dělla na nějakém pracovním listu, kde jsme už proměnné A měl použité tak miso A1 a A2 mam v a u, ale to na funkci rostlinaře nemá vliv.
S=solve( [v*sin(2*pi*f*x1)+u*cos(2*pi*f*x1)==y1,v*sin(2*pi*f*x2)+u*cos(2*pi*f*x2)==y2], v,u)
Offline
#10 11. 10. 2016 02:37
Re: Jak určit amplitudu a 0 funkce sinus?
↑ Berger:
To není zaokrouhlovací chyba!
Jak jsem napsal v příspěvku #6, ty dva zápisy jsou ekvivalentní (oba v sobě zahrnují amplitudu i počáteční fázový posuv, akorát ve druhém zápisu to není explicitní). Přechod od parametrů  k
k  je jednoduchý:
je jednoduchý: ,
, .
.
Obráceně, přechod od parametrů  k
k  bude
bude ,
, .
.
Použil jsem tebou uvedené dva body
x1=1/10E6*10
y1=1,339566987
x2=x1+1/10E6
y2=1,469463131
a vyšlo mi následující: ,
, .
.
Po převodu na amplitudu A a fázi P to dává: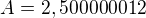 ,
,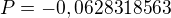 .
.
Otázka zůstává, zda jsi úmyslně použil na simulaci funkci, která neprochází bodem [0,0]. Jak je vidět, počáteční fázový posuv P odpovídá posunutí na ose x o jeden vzorek:
Offline
Stránky: 1
- Hlavní strana
- » Ostatní zajímavé dotazy a úlohy, dotazy pro praxi
- » Jak určit amplitudu a 0 funkce sinus?