Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 15. 10. 2016 20:33
Re: součet binomických čísel
Ahoj
Pozri si aj toto
https://sk.m.wikipedia.org/wiki/Binomická_veta
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



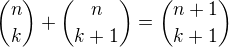
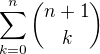 - všimni si, že k=0
- všimni si, že k=0 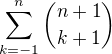 - k=-1, protože pak k+1 se pro k=-1 rovná nule tak, jako v původní sumě
- k=-1, protože pak k+1 se pro k=-1 rovná nule tak, jako v původní sumě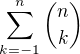 odebereme prvního sčítance pro k=-1: má tedy tvar
odebereme prvního sčítance pro k=-1: má tedy tvar 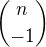 a zbylé sčtance pro další k=1, k=2, atd. ponecháme ve tvaru
a zbylé sčtance pro další k=1, k=2, atd. ponecháme ve tvaru 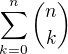
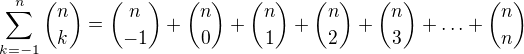
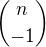 je vyjmut a celý další součet
je vyjmut a celý další součet 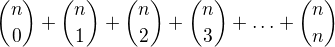 je nahrazen sumou
je nahrazen sumou 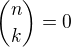 když k<0 nebo k>n.
když k<0 nebo k>n.