Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Funkce, DF, inverzni (TOTO TÉMA JE VYŘEŠENÉ)
#2 05. 01. 2008 23:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Funkce, DF, inverzni
(arccos(4x+1)) je v jmenovateli?
- pak nesmi byt rovny 0 a zaroven (4x+1) musi byt v intervalu <-1, 1>
pokud neni v jmenovateli, tak pouze druha podminka.
Pro inverzni funkci bych potrebovala upresnit, jak presne vypada zadani / staci slovne citatel ... jmenovatel ...
Offline
#4 05. 01. 2008 23:44 — Editoval jelena (05. 01. 2008 23:45)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Funkce, DF, inverzni
Okaz napsal(a):
takhle to je presnejsi
(1/2)(arccos(4x+1))
a jak pak teda v konecnym uctovani vypada to DF? Me funkce nikdy moc nesly

pak omezeni plyne pouze z arccos - vyraz (4x+1) musi byt v intervalu <-1, 1>
tj. resime soustavu nerovnic 4x+1<1 ^ 4x+1>-1
x bude nalezet intervalu <-0.5, 0>
Offline
#8 06. 01. 2008 00:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Funkce, DF, inverzni
To je tak - kazde plus ma sve minus, temer kazde deleni (az na 0) ma sve nasobeni, mocniny maji odmocniny (ten definicni obor se nam stale suzuje), exponencialni funkce maji logaritmy (definicni obor je jeste uzsi) a goniometricke funkce maji k sobe svoje arcusy.
Jednota a boj protikladu :-)
Offline
#10 06. 01. 2008 09:53
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Funkce, DF, inverzni
jelena napsal(a):
To je tak - kazde plus ma sve minus, temer kazde deleni (az na 0) ma sve nasobeni, mocniny maji odmocniny (ten definicni obor se nam stale suzuje), exponencialni funkce maji logaritmy (definicni obor je jeste uzsi) a goniometricke funkce maji k sobe svoje arcusy.
Jednota a boj protikladu :-)
já někdy říkám, že arccos je protijed na cos :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Funkce, DF, inverzni (TOTO TÉMA JE VYŘEŠENÉ)
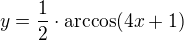 budeme vyjadrovat x
budeme vyjadrovat x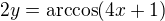
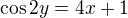
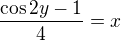 ted provedeme prejmenovani
ted provedeme prejmenovani 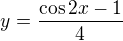 definicni obor inverzni funkce uz nebude problem, ze :-)
definicni obor inverzni funkce uz nebude problem, ze :-)