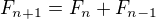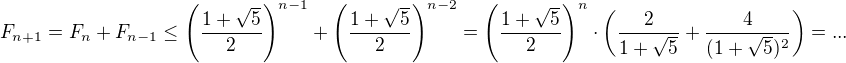Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz nerovnosti s fibonacciho posloupností (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 10. 2016 13:32 — Editoval ViliX (23. 10. 2016 13:42)
- ViliX
- Host
Důkaz nerovnosti s fibonacciho posloupností
Dokažte, že pro  platí
platí 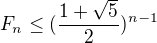 , kde
, kde 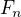 je n-tý člen fibonacciho posloupnosti definované:
je n-tý člen fibonacciho posloupnosti definované: 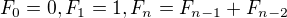
Začal jsem to řešit indukcí. Pro  nerovnost samozřejmě platí. Potíž mám s indukčním krokem.
nerovnost samozřejmě platí. Potíž mám s indukčním krokem.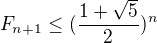
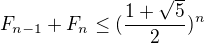
Tady mě napadlo, že jelikož  , tak se nerovnost nerozbije když to nahradím.
, tak se nerovnost nerozbije když to nahradím.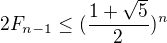
Zde jsem ale ve slepé uličce.
Taky jsem zkoušel toto: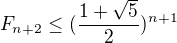
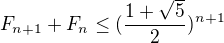
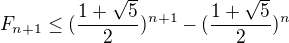
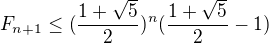
Ale to asi taky nikam nevede.
Moc děkuji za rady.
- (téma jako vyřešené označil(a) ViliX)
#3 23. 10. 2016 14:55
- ViliX
- Host
Re: Důkaz nerovnosti s fibonacciho posloupností
↑ holyduke:
Tady jsem se právě taky nacházel.
Má se dokázat, že 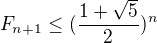 , ale ve vztahu je
, ale ve vztahu je 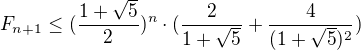
Omlouvám se pokud přehlížím něco zjevného.
#5 23. 10. 2016 15:08
- ViliX
- Host
Re: Důkaz nerovnosti s fibonacciho posloupností
↑ holyduke:
Nedošlo mi že to může být jednička. Moc děkuji.
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz nerovnosti s fibonacciho posloupností (TOTO TÉMA JE VYŘEŠENÉ)

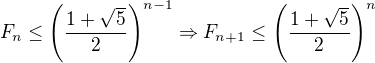 kde
kde