Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Irationalne cislo
#1 26. 10. 2016 18:46
Irationalne cislo
Casto sa stretneme z cvicenim ako:
Dokazte, ze 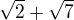 je irationalne cislo.
je irationalne cislo.
Iste poznate viacero dokazov.
Mozte nam ich tu pripomenut.
( jeden z nich sa mi celkom paci ... ak sa tu neobjavi tak vam ho tu pochopitelne dam)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 27. 10. 2016 18:06
Re: Irationalne cislo
Tak dobre.
Dam tu princip toho sympatickeho dokazu ( vieme,ze 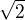 ako aj
ako aj 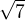 su irationalne)
su irationalne)
Mame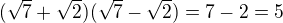
Sucin dvoch cisiel v zatvorke je racionale cislo, tak cisla v zatvorkach su zaroven obe racionalne alebo obe iracionalne.
Predpokladajme ze obe zatvorky su racionalne, tak polovica ich suctu ako aj polovica ich rozdielu su potom rationalne cisla.
Inac povedane 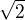 a tiez
a tiez 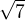 su racionalne. Ale to je spor. Cize nas predpokladu nie je pravdivy.
su racionalne. Ale to je spor. Cize nas predpokladu nie je pravdivy.
Co znamena ze  a tiez
a tiez 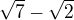 su oba iracionalne cisla.
su oba iracionalne cisla.
Mne sa zda, ze i ked ho casto nevidime takyto dokaz ma vyhodu, ze sa da pouzit aj pre deti na strednej skole.
Paci sa vam?
Pozname vela dokazov na ukazanie tohto vysledku. Poznate aj iny taky sympaticky?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 28. 10. 2016 22:34
Re: Irationalne cislo
↑ Andrejka3:
Nechť 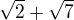 je racionální. Pak nutně
je racionální. Pak nutně 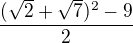 je racionální. Nicméně
je racionální. Nicméně 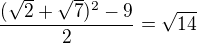 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 29. 10. 2016 09:44 — Editoval vanok (29. 10. 2016 09:57)
Re: Irationalne cislo
Pozdravujem,
Varianta od kolegu ↑ Pavel: je asi ta co kazdeho napadne ako prva.
A tato je tiez dost zriedkava, lahko overime, ze 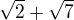 je koren
je koren 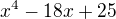 potom vysetrime ( klasicky ) jeho racionalne korene a
potom vysetrime ( klasicky ) jeho racionalne korene a 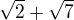 nie je medzi nimi.
nie je medzi nimi.
( otazka: viete nast take celociselne polynomy?)
Tento dokaz, na viac ukaze, ze nase cislo je algebraicke.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 29. 10. 2016 21:59 — Editoval vanok (29. 10. 2016 22:01)
Re: Irationalne cislo
Odpoved na otazku ↑ vanok:,
Oznacme nase cislo x,
Potom vyuzime co napisal ↑ Pavel:,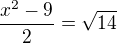
A to da po umocneni a uprave hladany polynom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 01. 11. 2016 17:39
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Irationalne cislo
↑ Pavel:
Ahoj, pěkné řešení, ale zvídavý student by se zeptal - proč volit právě výraz 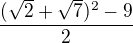 ? Podobné řešení s méně otazníky by mohlo být sporem - nechť
? Podobné řešení s méně otazníky by mohlo být sporem - nechť 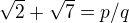 , tak umocněno na druhou a úpravou získáme
, tak umocněno na druhou a úpravou získáme 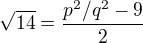 - a tedy jsme odvodili, že
- a tedy jsme odvodili, že 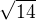 je racionální, což je spor.
je racionální, což je spor.
"Máte úhel beta." "No to nemám."
Offline
#8 01. 11. 2016 17:48
Re: Irationalne cislo
Ahoj ↑ check_drummer:,
Ano to je tiez velmi prirodzena moznost.
Tiez je velmi zaujimave porovnat rozdielne riesenia. A tiez vidiet na akej urovni su mozne?
Pri rieseniach ziak, student alebo aj vyucujuci moze dat rozne otazky. Ako napr. Sucet dvoch iracionalnych moze byt racionalny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Irationalne cislo
