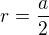Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 05. 2009 15:31
Slovní úloha
Takže jsem tu zase, ale tentokrát se slovní úlohou. Takže tady je zadání a prosil bych o nějaké vodítka.
Zadání: Půdorys divadelního jeviště je sjednocením obdélníku a půlkruhu. Obvod půdorysu je 40m. Určete rozměry půdorysu, víte-li, že byly stanoveny tak, aby obsah půdorysu jeviště byl co největší.
Offline
#2 03. 05. 2009 15:46 — Editoval svatý halogan (03. 05. 2009 16:29)
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Slovní úloha
Předpokládám, že kruh bude napojen na delší stranu (dejme tomu A) obdélníku a mohu tedy počítat, že obvod bude následující:
Máme tedy kvadratickou rovnici a zajímá nás, kde bude její extrém (resp. maximum). Ještě ale musíme za B dosadit vyjádřené B z rovnice obvodu.
Edit: samozřejmě /8, už jsem přemýšlel moc dopředu :)
Offline
#3 03. 05. 2009 15:55
Re: Slovní úloha
↑ svatý halogan:
Ale když už v celkovém obsahu počítám celý obdelník, neměl bych počítat už jen s polovinou obsahu kruhu? Takže by vzorec byl 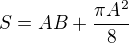 ?
?
Offline
#4 03. 05. 2009 16:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úloha
↑ LamaGanja:
u kolegy pravděpodobně jen drobny překlep, překontroluji si to - myslím, že tvoj návrh vzorce OK.
↑ svatý halogan: moc zdravím a děkuji :-) a opět zmiznu k tabulkam
Offline
#8 03. 05. 2009 16:44
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Slovní úloha

Teď to nějak zkondenzovat dohromady a derivovat klasicky podle x. Všechno ostatní jsou konstanty. Třeba vytkni x^2.
Offline
#9 03. 05. 2009 17:06
Re: Slovní úloha
↑ svatý halogan:
Takže mám  a první derivace je
a první derivace je  , z toho mám kořen
, z toho mám kořen  , ale nějak nechápu, co mi to pomůže k tomu, abych dostal hodnoty jednotlivých stran :(
, ale nějak nechápu, co mi to pomůže k tomu, abych dostal hodnoty jednotlivých stran :(
Offline
#10 03. 05. 2009 17:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovní úloha
↑ LamaGanja:
x jsme napsali misto A - tedy máš nalezenou stranu A. Výpocty jsem nekontrolovala.
Offline
#12 26. 02. 2018 18:14
Re: Slovní úloha
Ahoj, můžu poprosit zpětně o vysvětlení toho, proč je zde vzorec na obvod a obsah půdorysu uveden tak, jak je?
Mně vyšlo  , tedy od obvodu obdélníku jsem odečetl průměr kruhu a přičetl obvod půlkruhu.
, tedy od obvodu obdélníku jsem odečetl průměr kruhu a přičetl obvod půlkruhu.
Podobně mám obsah jako  , tedy k obsahu obdélníku jsem přičetl obsah půlkruhu.
, tedy k obsahu obdélníku jsem přičetl obsah půlkruhu.
Chápu, že vy zde to máte správně, ale než jen tupé přijmutí toho vzorce jako fakt bych rád znal jeho odvození. Možná je chyba v tom, že jsem si vše už v počátku špatně načrtl a chybně si tak půdorys představuji, nevím. Jedno je ale jisté - za použití těch mých dvou vzorečků to je (minimálně pro mě :D ) neřešitelné, mám tam o jednu neznámou v podobě poloměru navíc.
Offline
#14 26. 02. 2018 19:04
Re: Slovní úloha
↑ laszky:
Díky moc za odpověď.. Takže je to tak, jak jsem si to myslel, mám je špatnej náčrt :D
Bral jsem to tak, že ten půlkruh nemusí hned navazovat,že jeho průměr není celá strana, ale že je to jen takový výkroj ven.. Asi málo chodím do divadla, díky moc.. :D
Offline
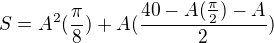 a co mám teď udělat?
a co mám teď udělat?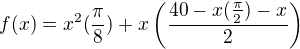
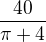 , takže to je polovina A a to by logicky i mohlo sedět, takže děkuji za pomoc.
, takže to je polovina A a to by logicky i mohlo sedět, takže děkuji za pomoc.