Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 11. 2016 14:33 — Editoval vanok (01. 11. 2016 14:36)
Prvocisla
Davat ulohy na ktorych riesenie by bolo treba cakat storocia, to nie je asi vitane na fore.
Ale toto cvicenie, vhodne pre studenta tak tretieho rocnika VS, (alebo aj kandidata na IMO) urcite niekoho zaujme.
Nech je n prirodzene neparne cislo take, ze 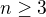
Dokazte, ze dva nasledujuce tvrdenia su ekvivalentne
(i)  a
a 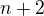 su prvocisla.
su prvocisla.
(ii)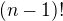 nie je delitelne ani cislom
nie je delitelne ani cislom  , ani cislom
, ani cislom 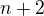 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 01. 11. 2016 23:56 — Editoval byk7 (02. 11. 2016 00:12)
Re: Prvocisla
Podle Wilsonovy věty platí  právě, když n je prvočíslo. Dále se lehce zdůvodní, že pro složené
právě, když n je prvočíslo. Dále se lehce zdůvodní, že pro složené  je
je  .
.
Tím pádem je vyřešená implikace (i) => (ii), a z opačné implikace máme "n nedělí (n-1)!, pak n je prvočíslo". Druhou část dokážeme obměnou. Řekněme, že je n+2 složené, pak n+2=ab, kde  , ale můžeme říct víc, je-li
, ale můžeme říct víc, je-li 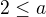 , pak
, pak  , tj. n+2 dělí (n-1)!.
, tj. n+2 dělí (n-1)!.
A jsme hotovi.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 02. 11. 2016 00:15
Re: Prvocisla
Ahoj ↑ byk7:,
Veta sme hotovi je trocha skratka.
Keby si mohol napisat detaily dokazov... tvoji kolegovia by boli ozaj radi.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
