Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 11. 2016 16:35
- dominiksep
- Příspěvky: 54
- Reputace: 0
Limita posloupnosti
Ahoj,
mohli byste mi prosím poradit, jak na limitu následující posloupnosti:![kopírovat do textarea $\lim_{n\rightarrow +\infty}n(\sqrt[n]{e}-1)$](/mathtex/fa/fad8934b7f86aec4869f351db8c3763a.gif)
Děkuji
Offline
#2 14. 11. 2016 16:51
Re: Limita posloupnosti
↑ dominiksep:
Ahoj, rozšiř zlomek výrazem  , potom za použití Heineovy věty a l'Hospitalova pravidla dostaneš výsledek.
, potom za použití Heineovy věty a l'Hospitalova pravidla dostaneš výsledek.
Offline
#3 14. 11. 2016 16:51
#4 14. 11. 2016 16:56
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Limita posloupnosti
↑ Pritt:
Tak bych to normálně řešil taky, ale nesmíme použít Heineovu větu a musíme tedy zůstat u posloupností.
Offline
#5 14. 11. 2016 21:46
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Limita posloupnosti
↑ Al1:
Ahoj,
to vede na substituci, ne? Ta ale jde udělat jen pro limitu funkce, jestli se nepletu. Já musím zůstat u posloupností.
Offline
#6 14. 11. 2016 22:32
Re: Limita posloupnosti
↑ dominiksep:
Ta substituce je vlastně Heineova věta. Jinak teď jiné řešení nevidím, tak snad doplní někdo jiný.
Offline
#7 16. 11. 2016 08:25
Offline
#9 19. 11. 2016 14:38 — Editoval jarrro (19. 11. 2016 14:41)
Re: Limita posloupnosti
↑ Pritt:veď práve neviem či je to vôbec pravda
Uvažoval som tak,že som položil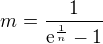 potom
potom![kopírovat do textarea $n\(\sqrt[n]{\mathrm{e}}-1\)=\frac{1}{\ln{\(1+\frac{1}{m}\)}}\cdot\frac{1}{m}$](/mathtex/1c/1ccbccdefe199b61366013b112be8b1d.gif)
Tu ale m nemusí byť prirodzené preto tie horné a dolné celé časti
To by sa potom mohla využiť veta o dvoch policajtoch (teda ak to platí )( lebo ak horná aj dolná časť m idú k nekonečnu tak aj n ide k nekonečnu) a spojitosť logaritmu.
MATH IS THE BEST!!!
Offline
#11 19. 11. 2016 19:14 — Editoval jarrro (19. 11. 2016 19:26)
Re: Limita posloupnosti
Pritt napsal(a):
Tak první část toho odhadu funguje.
Ale co ta druhá část?
Pokud, tak je výraz
, takže
a tedy
.
Což tedy ten odhad zpochybňuje, řekl bych.
Zabudol si ešte vynásobiť menovatele nie?
MATH IS THE BEST!!!
Offline

![kopírovat do textarea $\lim_{n\rightarrow +\infty}n(\sqrt[n]{e}-1)=\lim_{n\to\infty }\frac{e^{\frac{1}{n}}-1}{\frac{1}{n}}$](/mathtex/8b/8bf6292ae1698aa016bd818b6ad2c55e.gif)
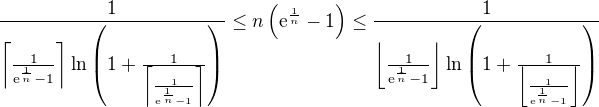
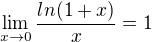 tak bych řekl, že jsme si moc nepomohli.
tak bych řekl, že jsme si moc nepomohli.