Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » předpis nekonečné posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#2 17. 11. 2016 11:17 — Editoval vanok (17. 11. 2016 11:19)
Re: předpis nekonečné posloupnosti
↑ aniuce:
Navod.
Toto by ta mohol inspirovat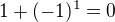
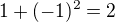 ...
...
A tiez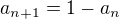 .....
.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 17. 11. 2016 18:07
Re: předpis nekonečné posloupnosti
↑ vlado_bb:,
Presne tak.
Povedzme, ze ide o na ucenie vdaka analogii.
Dat riesenie neda kolegini kapacitu ho dokazat najst aj v inych podobnych situaciach.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 17. 11. 2016 19:48
Re: předpis nekonečné posloupnosti
↑ aniuce:
A toto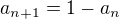
si pochopila?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 22. 11. 2016 16:47 — Editoval Rumburak (22. 11. 2016 16:48)
Re: předpis nekonečné posloupnosti
↑ aniuce:
Ahoj. Zdravím i ostatní "účinkující" .
Uvědom si, že s číselnými posloupnostmi (obecněji s číselnými funkcemi) můžeme provádět i různé
algebraické operace.
Například součtem takových posloupností  , kde
, kde  probíhá množinu všech
probíhá množinu všech
přirozených čísel, je posloupnost 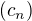 , jejíž n-tý člen je definován předpisem
, jejíž n-tý člen je definován předpisem 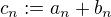 .
.
Obdobně možno uplatnit i alg. operace další (samozřejmě v rámci jejich definičních oborů),
v Tvé úloze se třeba hodilo násobení posloupnosti konstantou.
Offline
#13 22. 11. 2016 18:02
Re: předpis nekonečné posloupnosti
Pozdravujem vsetkych kolegov.
Poznamka, mozno pomoze....
Ako ↑ vlado_bb:, ↑ vanok:, ↑ Rumburak:
vsetci cakali, ze pytatelka nam povie, ze akoze ste mi poradili nast relaciu danu indukciou, tak ( sme cakali, ze sa nam podakuje za takuto radu ) A nam povie, ze moja indukcia zacina prvym clenom ( 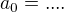 ), ktoru pridam ku kompletnej definicii.
), ktoru pridam ku kompletnej definicii.
Je to ako skusit dokazovat indukcne dokazy bez inicialneho kroku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 23. 11. 2016 16:09
Re: předpis nekonečné posloupnosti
Ahoj ↑ aniuce:,
No musis overit, ze to sedi.
Ze mas dobre urcene 
A potom ze ta relacia 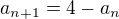 ti da cakane hodnoty.
ti da cakane hodnoty.
Kludne to mozes volât mini dokaz na overenie vzorca daneho indukciou ( alebo najdeneho...)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » předpis nekonečné posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)

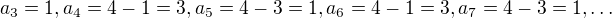 , a teda nejde o postupnost 0,4,0,4,0,4,0,... ale o postupnost 1,3,1,3,1,3,1,3,... ?
, a teda nejde o postupnost 0,4,0,4,0,4,0,... ale o postupnost 1,3,1,3,1,3,1,3,... ?