Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » "Neurcita limita"
#2 29. 12. 2016 21:23
Offline
#3 29. 12. 2016 21:34
Re: "Neurcita limita"
↑ vytautas:,
Najdi chybu v tvojom pokus o dokaz.
Akoze, som dal toto cvicenie do didaktiky, nie je to nahoda. Sluzi na to, aby sa na nom dalo poucit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 30. 12. 2016 12:44
Re: "Neurcita limita"
↑ vytautas:,
Vidim, ze si nenasiel tvoju chybu.
Tak je v tejto casti tvojho pokusu o riesenie
pretože výraz
ide k
podľa vety o limite zloženej funkcie
.
Vies ju analyzovat?
Ina konstatacia.
V tomto cviceni sa neda pouzit l'Hopitalove pravidlo. Preco?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 30. 12. 2016 13:42
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Offline
#6 30. 12. 2016 14:22
Re: "Neurcita limita"
Pozdravujem ↑ check_drummer:,
Ano to je dobre riesenie.
Dufajme, ze toto vlakno bude uzitocne pre vela jeho citatelov.
Vsetko pozitivne do Noveho Roku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 30. 12. 2016 23:21
Re: "Neurcita limita"
↑ vanok:
Predpoklady vety o zloženej funkcii sú, že ak  potom, ak existuje okolie, kde
potom, ak existuje okolie, kde  a ďalej ak
a ďalej ak 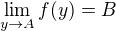 ,tak potom
,tak potom  .
.
v tomto prípade, ak x ide sprava k 0, tak vychádza  a zľava
a zľava  a keď si zoberiem
a keď si zoberiem 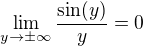 , pretože je to obmedzená krát nulová funkcia. je to takto správne ?
, pretože je to obmedzená krát nulová funkcia. je to takto správne ?
Per aspera ad astra
Offline
#8 31. 12. 2016 00:24 — Editoval vanok (31. 12. 2016 00:25)
Re: "Neurcita limita"
↑ vytautas:,
Ano, no vsak staci metoda co pouzil kolega ↑ check_drummer:.
A este, co sa tyka l'Hopitaloveho pravidla, tu sa neda pouzit, lebo derivacia vyrazu 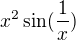 nema limitu v nule.
nema limitu v nule.
Vela uspechov v novom roku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » "Neurcita limita"

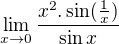 .
.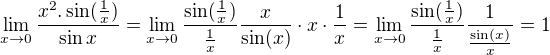
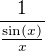 ide k
ide k 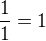 a celkovo teda ide výraz k
a celkovo teda ide výraz k