Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 01. 2017 23:55
L. algebra - inverzní matice
Ahoj,
V každé literatuře, do které jsem se podíval (skripta mff uk, fel čvut, fjfi čvut, mit, linear algebra and its applications) jsem našel definici inverzní matice: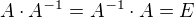 ,
,
kde E je jednotková matice.
Myslím si, že stačí: ,
,
protože: (0 - nulová matice)
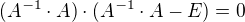
(hodnost = rank)
A i inv(A) jsou regulární, násobením reg maticí se nemění hodnost, proto hodnost 2. závorky je rovna levé straně - 0, takže je to nulová matice, proto: .
.
Otázka je tedy následující: Buď mám někde chybu, proto prosím o korekci, jinak proč je v definici zbytečná část?
Děkuji
Offline
#2 14. 01. 2017 01:23
Re: L. algebra - inverzní matice
Ahoj ↑ Vašek:,
Staci jednoduchsie pracovat vo structure grupy.
Konkretne.
Prestuduj podrobne axiomy tejto structury a najdi, co najjednoduchsie axiomy tejto struktury.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 14. 01. 2017 08:56
Re: L. algebra - inverzní matice
Pri štvorcových maticiach je to pravda. Definícia sa vzťahuje na všetky matice ( ale sa dá dokázať , že aby mohla matica mať inverziu pri štandardnej definícii tak musí byť štvorcová.) Pri vynechaní otočenia poradia by mali aj niektoré neštvorcové matice inverziu
MATH IS THE BEST!!!
Offline
