Matematické Fórum

aoiffe · 19. 01. 2017 20:01

Ahoj. Prosím o radu. Mám zadané uzly (body) a mám zjistit, které z polynomů jsou fundamentální polynomy pro tvorbu lagrangeova tvaru interpolačního polynomů, ale bez počítání. Umím je spočítat, ale nevím, jak je mám vybrat bez počítání. Děkuji.

Body: [-1;2] [0;3] [2;-1] [3;2] [-2;4]

Polynomy na výběr:

1/12(x^4 + x^3 - x^2 + 4x)

1/60(^4 + x^3 - 4x^2 + 4x)

1/40(2x^4 - x^3 + x^2 + x -2)

1/12(x^4 - 2x^3 - 7x^2 + 8x + 12)

aoiffe · 19. 01. 2017 20:51

Toto je postup a řešení. Zadaný mám horní červený rámeček. Možnosti jsou ve druhém rámečku. Potřebuji zjistit výsledky bez počítání. Poradil by někdo prosím? Děkuji moc.

//forum.matweb.cz/upload3/img/2017-01/55428_POLYNOM.png

jelena · 19. 01. 2017 22:31

Zdravím,

zkus se podívat např. na materiál v odkazu (str. 19), uvědomit si, jak od Tvých polynomů přejít k funkci 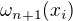$\omega_{n+1}(x_i)$ ve vhodně zvoleném x ze zadaných bodů a jak potom bude vypadat "zkouška jmenovatele". Pomůže tak (pro odvození "pomůcky" buď materiál v odkazu nebo podrobněji váš)? Děkuji.

Eratosthenes · 19. 01. 2017 22:33

ahoj ↑ aoiffe:,

sice nevím přesně, co znamená "bez počítání", ale pokud to má být "bez počítání", tak to zelené určitě zahoď. - to je totiž výpočet. Aby nějaký polynom byl pro danou tabulku bázový, tak musí procházet právě jedním tabulkovým bodem, pro ostatní x-ové souřadnice musí vycházet nula. Třeba první polynom to určitě není, protože pro x=-1 mi vychází -5/12, což není ani 2, ani nula.

Úplně bez počítání to sice není, ale jinak mě nic nenapadá.

aoiffe · 20. 01. 2017 19:38

jelena: Děkuji za odpověď. Bohužel polynomy vůbec nebude čas počítat. Mám pouze zadanou tabulku a určit výsledky bez počítání polynomů.

Eratosthenes: Děkuji moc! Přesně to jsem potřebovala. Zadání bylo myšleno asi jen bez počítání polynomů. Ten výpočet jsem připojila, aby to pomohlo k odpovědi. Nedokázala jsem z něj odvodit, jak by se dalo přijít na výsledek, aniž bych polynomy počítala. Ještě jednou díky :-)

Matematické Fórum

#1 19. 01. 2017 20:01

Lagrangeův tvar interpolačního polynomu

#2 19. 01. 2017 20:51

Re: Lagrangeův tvar interpolačního polynomu

#3 19. 01. 2017 22:31

Re: Lagrangeův tvar interpolačního polynomu

#4 19. 01. 2017 22:33

Re: Lagrangeův tvar interpolačního polynomu

#5 20. 01. 2017 19:38

Re: Lagrangeův tvar interpolačního polynomu

#6 21. 01. 2017 16:22 Příspěvek uživatele aoiffe byl skryt uživatelem aoiffe.

Zápatí