Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2009 15:06
- mankindzero
- Zelenáč
- Příspěvky: 2
- Reputace: 0
Goniometricka rovnica
zdravim,
potreboval by som poradit s nasledujucou rovnicou, riesenie ma byt v intervale
vdaka
Offline
#2 09. 05. 2009 15:34
Offline
#4 09. 05. 2009 15:53
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Goniometricka rovnica
↑ gadgetka:
když máš 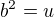 , tak po odmocnění to je
, tak po odmocnění to je 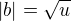 .
.
Navíc napřed máš jeden kořen, pak se tam objeví náhle druhý :)
Offline
#5 09. 05. 2009 15:54
#6 09. 05. 2009 16:02
Re: Goniometricka rovnica
wow, původně jsem měla připsáno, že zbytek si tazatel udělá jistě sám, jak jsem příklad upravovala, tento dovětek jsem vymazala ... a nakonec na začátku jsem psala "nápověda" ... takže se omlouvám, konec svého příspěvku máznu, tazatel si to jistě správně dokončí sám :))
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 09. 05. 2009 16:18
Re: Goniometricka rovnica
↑ svatý halogan:mohla bych se zeptat, proč jsou ty výsledky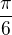 ...
...
vždyť přece 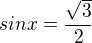
pak by to mělo být 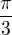 ...
...
Offline
#9 09. 05. 2009 16:31
- mankindzero
- Zelenáč
- Příspěvky: 2
- Reputace: 0
Re: Goniometricka rovnica
diky, na tu substituciu som nevedel prist :)
Offline
#10 09. 05. 2009 16:31
Re: Goniometricka rovnica
↑ gadgetka: na substituci jsem zapomněla, takže ten výsledek >> pí/3 ještě vydělím 2 >> chápu to dobře??
Offline
#11 09. 05. 2009 16:32
#13 09. 05. 2009 16:35
Offline
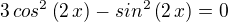
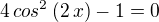
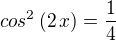

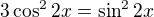
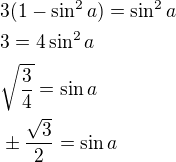
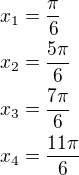
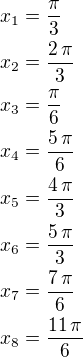
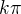 , oki?
, oki?