Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 02. 2017 19:05
Parciální derivace, příklad – substituce
Zdravím,
potřeboval bych pomoci s jedním příkladem. Třeba derivaci podle x, z f(x,y) = ln (x + (x^2 + y^2)^(1/2)) jedná se mi o první derivaci. Zbytek bych měl nějak doupravit a dopočítat, děkuji Filip.
Offline
#2 28. 02. 2017 19:09 — Editoval ViliX (28. 02. 2017 19:15)
- ViliX
- Host
Re: Parciální derivace, příklad – substituce
Vychází mi to: 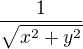 , nejsem si však jistý. Řešil jsem to za použití pravidla pro derivaci složené funkce a logaritmu.
, nejsem si však jistý. Řešil jsem to za použití pravidla pro derivaci složené funkce a logaritmu.
#3 28. 02. 2017 19:14
- ViliX
- Host
Re: Parciální derivace, příklad – substituce
Takto jsem na to šel: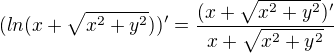

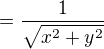
#8 28. 02. 2017 19:24
- ViliX
- Host
Re: Parciální derivace, příklad – substituce

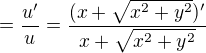
#10 28. 02. 2017 19:34
- ViliX
- Host
Re: Parciální derivace, příklad – substituce
Obecně derivace složených funkcí funguje takto: 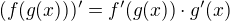
Uvažme teď jednodušší příklad než máš ty: 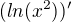
Zderivuji první vnější funkci a pak vynásobím derivací vnitřní funkce: 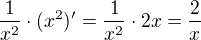
#12 28. 02. 2017 19:36
- ViliX
- Host
Re: Parciální derivace, příklad – substituce
Jo tak. Obecně, jak by jsi zderivoval:  ?
?
#14 28. 02. 2017 19:39
- ViliX
- Host
Re: Parciální derivace, příklad – substituce
↑ Filip2142:
Každý se musí věcem někdy naučit. Není třeba se kát :) Jsem rád že tomu už rozumíš.
