Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 14. 03. 2017 18:03
Re: Logaritmus
↑ zdenek1:
Zdravím,
od které doby je v pravidlech předložení úplného řešení? Nestačilo napsat, že se rovnice řeší logaritmováním? A vyčkat na reakci?
Offline
#4 14. 03. 2017 18:40
Re: Logaritmus
↑ Al1:
Možná, že stačilo.
Jenže dotaz byl původně v sekci ZŠ a já si nebyl jistý, jestli se jen tazatel/ka netrefil do správné sekce, nebo se jedná o zvídavého základoškoláka (i takové věci se stávají).
A takto mi to přišlo jednodušší, než to zjišťovat.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
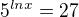

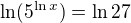
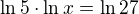
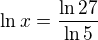
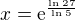
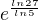 se dopočítám, ale ve výsledku má být
se dopočítám, ale ve výsledku má být 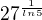
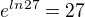 ?
?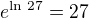 platí
platí