Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 15. 03. 2017 14:48 — Editoval Cheop (15. 03. 2017 14:51)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: rovnice
↑ aniuce:
No pak do kubické rovnice dosadíš druhý kořen x = 6 a dostaneš rovnici kvadratickou.
PS:
Nejdříve původní polynom vydělíš výrazem (x-1) a pak ten vypočtený podělíš výrazem(x-6) a to
už dostaneš kvadratickou rovnici, kterou vyřešíš "klasicky".
Nikdo není dokonalý
Offline
#8 15. 03. 2017 16:13 — Editoval vanok (15. 03. 2017 16:14)
Re: rovnice
Ahoj ↑ aniuce:,
Pokial poznas vetu o racionalnych (=evidentnych) korenoch tak je to jednoduche. Pozri tu https://en.m.wikipedia.org/wiki/Rational_root
Uci sa to v prvom rocnikovu VS (pred casom aj na SS).
Ide o uzitocnu vetu!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 16. 03. 2017 11:30 — Editoval vanok (16. 03. 2017 11:39)
Re: rovnice
Vsak si precitaj odkaz ↑ vanok:,
Presne mas
"p is an integer factor of the constant term  , and
, and
q is an integer factor of the leading coefficient  ."
."
Kde polynom je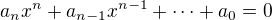
Tvojom cviceni 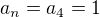 a
a 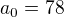
Tak, ak dany polynom ma nejaky cely koren, tak ten musi byt delitelom cisla 78.( kladne alebo zaporne)
Tak vidis, ze pripadne cele delitele tvojho polynomu musia byt medzi {1,-1,2,-2,... } napis ich vsetki a vyskusaj ...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 16. 03. 2017 16:05
Re: rovnice
Poznamka, toto vysetrenie ti podvrdi, ze mas tu dva cele korene: 1 a 6.
Po uplnom vysetreni podla tejto vety, mozes byt isty, ze dva zvysne korene nemozu byt cele.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline