Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 05. 2009 20:26
Pravidelný 8-boký jehlan
Ahoj.Máme DÚ z matematiky a já jaksi taksi nevím, jak na něj.Zadání zní: Pravidelný 8-boký jehlan- a=3cm;v=5,5cm;S=? ;V=?
;V=?.png) .
.
Pokud by mi někdo mohl napsat přesný postup, byl bych Vám vážně vděčnej:).Možná je to jednoduchý, ale na matiku jsem fakt dřevo:)
>Špenát<
"Dvě věci jsou nekonečné-vesmír a lidská hloupost.Ale u vesmíru to není úplně jisté"-Albert Einstein
Offline
#2 10. 05. 2009 21:08
Re: Pravidelný 8-boký jehlan
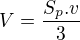 obsah podstava- osmiuhelník lze rozdelit na 8 shodných trojúhelnínů ve kterých znáš všechny úhly a jednu stranu, a víš že jsou rovnoramenné, velikost uhlu u středu je
obsah podstava- osmiuhelník lze rozdelit na 8 shodných trojúhelnínů ve kterých znáš všechny úhly a jednu stranu, a víš že jsou rovnoramenné, velikost uhlu u středu je 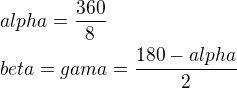 pak stačí použít sinovou větu a vzorec pro obsah trojúhelníku
pak stačí použít sinovou větu a vzorec pro obsah trojúhelníku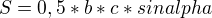
R. P. Feynman:Fyzika je jako sex, může přinést praktické výsledky, ale to není důvod, proč to děláme.
Offline
#3 10. 05. 2009 21:56
Re: Pravidelný 8-boký jehlan
Díky moc za rychlou odpověď, ale nějak nechápu: 1.)K čemu jsou potřeba úhly Alfa, Beta a Gama a za 2.)Nějak nerozumim tomu vzorci obsahu...
>Špenát<
"Dvě věci jsou nekonečné-vesmír a lidská hloupost.Ale u vesmíru to není úplně jisté"-Albert Einstein
Offline
#5 10. 05. 2009 22:01
Re: Pravidelný 8-boký jehlan
nebo:
u jednoho z osmi shodných rovnoramenných trojúhelníků, které tvoří podstavu, znáš stranu a a proti ní ležící středový úhel 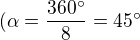 ), výška trojúhelníku ti onen trojúhelník rozdělí na dva pravoúhlé, s úhlem
), výška trojúhelníku ti onen trojúhelník rozdělí na dva pravoúhlé, s úhlem 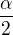 a protější stranou
a protější stranou 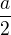 , přilehlou stranou je neznámá výška (x) rovnoramenného trojúhelníku;
, přilehlou stranou je neznámá výška (x) rovnoramenného trojúhelníku;
platí:
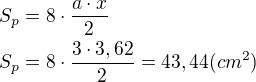

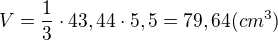
Stěnovou výšku vypočítáme pomocí Pythagorovy věty: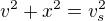
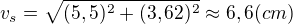
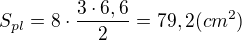
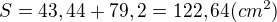
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#6 10. 05. 2009 22:06
Re: Pravidelný 8-boký jehlan
↑ spenat:
Vzorec obsahu:
U všech druhů jehlanů platí, že objem je velikost plochy podstavy krát jeho výška děleno třemi.
K výpočtu povrchu.
Vypočti si plochu podstavy (zde osmiúhelník). A k tomu přičti 8x plochu každé boční stěny (bude to rovnostranný trojúhelník o jedné straně "a" druhou si dopočítáš podle Pythagorovy věty).
Offline
#8 11. 05. 2009 16:22 — Editoval spenat (11. 05. 2009 16:34)
Re: Pravidelný 8-boký jehlan
Díky všem, vyřešeno a už to konečně chápu :-).A pokud jde o tu sinovu větu, tak Goniometrické fce už mám za sebou :-)
>Špenát<
"Dvě věci jsou nekonečné-vesmír a lidská hloupost.Ale u vesmíru to není úplně jisté"-Albert Einstein
Offline
