Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Rozdělení přímky zadaným počtem rovnobězek (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 04. 2017 16:41 — Editoval Hax (15. 04. 2017 16:42)
Rozdělení přímky zadaným počtem rovnobězek
Zdravím,
Mám zadanou přímku y = a.x +b (znám a a b). Na ose x si zvolím libovolně velikou vzdálenost AB. Na danou vzdálenost se musí vměstnat n rovnoběžek, které mají zápornou směrnici a v první rovnoběžka protíná přímku v f(A) a osu X v bodě X1 druhá rovnoběžka protne přímku v f(X1) a vytvoří bod X2... tohle se opakuje n krát. Až poslední rovnoběžka protne osu X v bodě B.
Je možné nějak zjistit směrnice těchto rovnoběžek?
Pokud se nepletu. A to je často.
Offline
- (téma jako vyřešené označil(a) Hax)
#4 16. 04. 2017 10:22
- Eratosthenes
- Příspěvky: 2844
- Reputace: 137
Re: Rozdělení přímky zadaným počtem rovnobězek
ahoj ↑ Hax:,
je to celé nějaké divné. Co je f?
Budoucnost patří aluminiu.
Offline
#5 16. 04. 2017 12:07 — Editoval misaH (16. 04. 2017 12:07)
- misaH
- Příspěvky: 13459
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Eratosthenes:
y=f(x) je tá priamka. f(A) je potom hodnota y pre x=A (myslí sa ixová hodnota bodu A).
Offline
#6 16. 04. 2017 12:11
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Eratosthenes:
Funkční hodnota v bodě. Na přímce y = ax + b.
Pokud se nepletu. A to je často.
Offline
#8 16. 04. 2017 12:26
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ misaH:
Je to zapeklité z prvu mi to připadalo, že by to šlo vyřešit s podobností trojúhelníku jelikož všechny úhly rovnoběžek musí být stejné. Nicméně jsem se dostal do problému že jsem měl více neznámých než rovnic a na nové rovnice jsem nemohl přijít.
Pokud se nepletu. A to je často.
Offline
#9 16. 04. 2017 14:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozdělení přímky zadaným počtem rovnobězek
Zdravím,
↑ Hax: pokud si dobře představuji to, co popisuješ, potom by snad šlo využit geometrickou posloupnost (vepsané trojúhelníky jsou si podobné a něco mi říká, že geometrická posloupnost by platit měla). Potom by šlo použit vzorec pro součet  členů posloupnosti pro úsečky, co odseknout rovnoběžky na délce |AB| (jsou 2 neznámé
členů posloupnosti pro úsečky, co odseknout rovnoběžky na délce |AB| (jsou 2 neznámé  ,
,  ) a zároveň platí vztah mezi prvním pravoúhlým trojúhelníkem s odvěsnou vycházející z bodu A a posledním pravoúhlým trojúhelníkem, co dostrojíme "navíc" s odvěsnou vycházející z bodu B. Zde budeme uvažovat (n+1) členů a vztah mezi prvním a posledním členem (délky odvěsen známe), ze kterého najdeme
) a zároveň platí vztah mezi prvním pravoúhlým trojúhelníkem s odvěsnou vycházející z bodu A a posledním pravoúhlým trojúhelníkem, co dostrojíme "navíc" s odvěsnou vycházející z bodu B. Zde budeme uvažovat (n+1) členů a vztah mezi prvním a posledním členem (délky odvěsen známe), ze kterého najdeme  a následně
a následně  .
.
Tím je dán první pravoúhlý trojúhelník a tedy směrnice rovnoběžky, která tvoří odvěsnou.
Zkus si to, prosím, promyslet, zatím jsem si to jen náznakem načrtla (podstatné je potvrdit, že jde o geometrickou posloupnost). Jak vznikl problém? Děkuji.
Offline
#10 16. 04. 2017 14:48
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ jelena:
Zdravím,
geometrická posloupnost to je zajimavý úhel pohledu.
Tento problém vznikl velmi jednoduše. Vymyslel jsem si ho nevím jestli ma řešení a ani nevím jak to dokázat (neumím matematické důkazy). Nicméně mi to přišla jako pěkná rekráční matematika.
Jsem si hral s geogebrou...
Takhle by to mělo vypadat pro n = 2 chtěl jsem to zobecnit na n.
Pokud se nepletu. A to je často.
Offline
#11 16. 04. 2017 19:29
- Eratosthenes
- Příspěvky: 2844
- Reputace: 137
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Hax:
takže pokud tomu dobře rozumím - zvolíš si A; B; n. Napálíš tam n rovnoběžek a potřebuješ vyjádřit jejich směrnici pomocí AB a n. Je to tak?
Budoucnost patří aluminiu.
Offline
#12 16. 04. 2017 20:28
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Eratosthenes:
Ano přesně a rovněž znám funkci y = ax + b
Pokud se nepletu. A to je často.
Offline
#13 16. 04. 2017 22:06
- Eratosthenes
- Příspěvky: 2844
- Reputace: 137
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Hax:
V tom případě by to nemělo být příliš těžké. Stejně jako ↑ jelena: bych tam viděl geometrickou posloupnost, přesněji řečeno dvě:
První posloupnost má první člen (dle Tvého obrázku) a, n+1 člen je d. Odtud zjistíš q.
Druhá posloupnost je posloupnost n+1 úseček na ose x (popř. na zadané přímce), která má stejné q a známý součet (buď CD, anebo AB - podle toho kterou si vybereš). Odtud zjistíš velikosti příslušných úseček a zbytek už je zřejmý.
Budoucnost patří aluminiu.
Offline
#14 16. 04. 2017 23:06
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Eratosthenes:
Díky,
Všem budu o tom přemýšlet.
Pokud se nepletu. A to je často.
Offline
#18 16. 04. 2017 23:30
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ misaH:
No to jsem to moc nepochopil, ale předpokládám že dojdu ke stejnému problémů jaký popisujete.
Nicméně jsem zjistil že geogebra není tak přesná a že rovnice budou lepší.
Pokud se nepletu. A to je často.
Offline
#21 17. 04. 2017 09:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rozdělení přímky zadaným počtem rovnobězek
Zdravím,
↑ jarrro: nejde ale tento Tvůj zápis 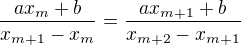 přepsat na
přepsat na 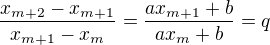
tedy, že poměry funkčních hodnot a poměry délek úseček na ose x (v součtu dávají |AB|) jsou stejné a svou geometrickou posloupnost tvoří funkční hodnoty, další geometrickou posloupnost tvoří úsečky na ose x. Kvocient je stejný  , první člen je ale jiný pro každou posloupnost. Viz ↑ příspěvek 9: a ↑ příspěvek 13: (akorát musím být důslednější v počtu členů - pokud je rovnoběžek
, první člen je ale jiný pro každou posloupnost. Viz ↑ příspěvek 9: a ↑ příspěvek 13: (akorát musím být důslednější v počtu členů - pokud je rovnoběžek  , potom je úseček na AB
, potom je úseček na AB 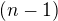 , ale funkčních hodnot, využívaných pro posloupnost je
, ale funkčních hodnot, využívaných pro posloupnost je  ).
).
Jak to vidíš? Děkuji.
Offline
#22 17. 04. 2017 09:35 — Editoval jarrro (17. 04. 2017 09:52)
Re: Rozdělení přímky zadaným počtem rovnobězek
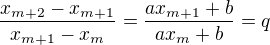
Je pravda .
z toho dostaneme keď označíme

Teda 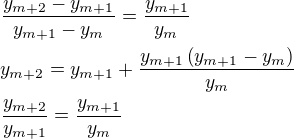
Dúfam, že nepíšem bludy.
P.S. Aha ja som troťo. geometrická je postupnosť dĺžok úsečiek vzniknutých na ose x daným delením. Ja som hľadal samotné body ktoré ako vidno geometrickú postupnosť netvoria.
Už som si myslel že mi šibe , ale každý mal pravdu
MATH IS THE BEST!!!
Offline
#23 17. 04. 2017 10:34 — Editoval Eratosthenes (17. 04. 2017 10:38)
- Eratosthenes
- Příspěvky: 2844
- Reputace: 137
Re: Rozdělení přímky zadaným počtem rovnobězek
ahoj ↑ misaH:↑ jarrro:↑ Hax:,
nevím, co dělá geogebra, ani jsem nic nepočítal. Ale je zřejmé, že mezi osou x a přímkou y=ax+b musí "pracovat" stejnolehlost se středem S v průsečíku přímky s osou x a koeficientem q:
Takže poměr q musí fungovat úplně na všem: na červeno zeleně rozstříhané ose x, modro žlutě rozstříhané přímce y=ax+b, růžových kolmicích i na hnědých rovnoběžkách. Takže jde jen o to, zjistit to q ze zadaných bodů A, B, C, D a daného n.
Budoucnost patří aluminiu.
Offline
#25 17. 04. 2017 10:45 — Editoval Hax (17. 04. 2017 10:46)
Re: Rozdělení přímky zadaným počtem rovnobězek
↑ Eratosthenes:
Zdravím,
Přesně o to se usiluje.
Pokud se nepletu. A to je často.
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Rozdělení přímky zadaným počtem rovnobězek (TOTO TÉMA JE VYŘEŠENÉ)