Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#11 23. 03. 2012 11:15 — Editoval Rumburak (23. 03. 2012 11:31)
Re: parciální derivace
↑ 0manrike:
U výrazů tvaru 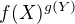 (kde i X, Y případně mohou být funkce), se nejprve použije úprava
(kde i X, Y případně mohou být funkce), se nejprve použije úprava
a tím se z toho "udělá" složená funkce (kde vnější funkcí je exponenciální funkce, vnitřní funkcí je součin 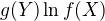 ) ,
) ,
což umožní použít používat věty o počítání limit resp. derivací složených funkcí.
Tak například věta o derivaci složené funkce 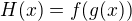 říká, že
říká, že 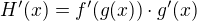 (za příslušných předpokladů).
(za příslušných předpokladů).
Pří tom symbol 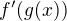 nutno číst tak, že do
nutno číst tak, že do 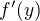 (což je derivace funkce f v bodě y) dosadíme y = g(x) .
(což je derivace funkce f v bodě y) dosadíme y = g(x) .
Speciálně  (protože
(protože  ).
).
Offline
#12 02. 04. 2013 13:36
- charlotte771

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: parciální derivace
Zdravím, potřebovala bych kontrolu výpočtu, zderivovat funkci zderivovat podle c2
(c1*x+c2*sin(x)-y)^2=0
děkuji
Offline
#13 02. 04. 2013 15:41
#15 19. 05. 2014 19:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: parciální derivace
↑ onyx:
Zdravím,
ze zápisu není úplně jasné, co se má počítat a co vyjadřovat - založ si, prosím, vlastní téma viz pravidla, překontroluj zadání + použij TeX pro zápis (Editor je napravo od okna zprávy). Děkuji.
nedokáže mi někdo spočítat následující?
toto není účelem fóra - spíš prodiskutovat Tvůj problém, abys ho dokázal spočítat samostatně.
Offline
#16 25. 03. 2015 20:08 — Editoval nikoletta1 (25. 03. 2015 20:12) Příspěvek uživatele nikoletta1 byl skryt uživatelem nikoletta1.
#17 01. 05. 2017 20:13 — Editoval hcdady (01. 05. 2017 20:15)
Re: parciální derivace
Dobrý večer, trošku tápu v parciálních derivacích tak bych se chtěl zeptat jestli na to jdu dobře.
Je zadána funce 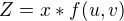 ,
,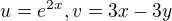 a je potřeba spočítat
a je potřeba spočítat  . Napadá mě tohle řešení jako derivace součinu.
. Napadá mě tohle řešení jako derivace součinu.![kopírovat do textarea $\frac{\delta z}{\delta x}=1*(\frac{\delta z}{\delta u}+\frac{\delta z}{\delta v})+x*[\frac{\delta z}{\delta u}*\frac{\delta u}{\delta x}+\frac{\delta z}{\delta v}*\frac{\delta v}{\delta x}]$](/mathtex/c6/c6bbb1101c9487b65aa2201bc9a643a7.gif)
z čehož po dosazení mi vyšlo![kopírovat do textarea $\frac{\delta z}{\delta x}=1*(\frac{\delta f}{\delta u}+\frac{\delta f}{\delta v})+x*[\frac{\delta f}{\delta u}*2e^{2x}-3\frac{\delta f}{\delta v}]$](/mathtex/d3/d375976746326b1e6876765b1b49792c.gif)
a nebo jsem úplně mimo.
Za ochotu předem díky.
Offline
#20 22. 04. 2021 20:49
- Nikolajvjb

- Zelenáč
- Příspěvky: 1
- Škola: Szsvzs
- Pozice: Student
- Reputace: 0
Re: parciální derivace
4f1x (1,1)+f1y(1,1), je-li f(x,y)=odmocnina1+3xdeleno x2
Offline
#21 22. 04. 2021 22:25 — Editoval Ferdish (22. 04. 2021 22:26)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: parciální derivace
↑ Nikolajvjb:
Prosím, ako prvé si založ na svoj dotaz vlastnú tému v správnej sekcii a pri tej príležitosti tiež odporúčam preštudovať pravidlá, nech to vyzerá ako prosba a nie ako rozkaz. Ďakujem.
Offline
#22 29. 04. 2021 14:45
Re: parciální derivace
↑ symetrala: Parciální derivace se dělají tak, že derivuješ jen dle dané proměnné a všechno ostatní jsou pro tebe konstanty. Zkus mrknout na tohle video, jsou tam sice i derivace druhého řádu, ale k tomu asi brzo taky dojdete ve škole ;-) https://youtu.be/NE7yzct-E0M
Offline
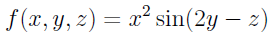
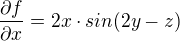 tohle je derivace podle "x"
tohle je derivace podle "x"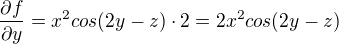 toto derivace podle "y"
toto derivace podle "y"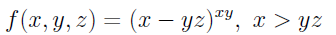
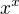 takže se to musí přepsat pomocí exponenciální funkce (jenom jako příklad pro pochopení
takže se to musí přepsat pomocí exponenciální funkce (jenom jako příklad pro pochopení 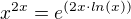 ) tedy:
) tedy: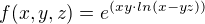 potom
potom![kopírovat do textarea $\frac{\partial f}{\partial x}=e^{(xy\cdot ln(x-yz))}\cdot [y\cdot ln(x-yz)+\frac{xy}{x-yz}]$](/mathtex/b1/b11b9424ef8713292b8d6959a7c523bb.gif)
![kopírovat do textarea $\frac{\partial f}{\partial y}=e^{(xy\cdot ln(x-yz))}\cdot [x\cdot ln(x-yz)+\frac{xy}{x-yz}\cdot (-z)]$](/mathtex/ad/adc0da590e18f5ebc007b0f94cfe6b06.gif)
