Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 17. 04. 2017 22:25
Re: Osy, pomery
Ahoj ↑↑ akdar:,
Vyborne. Dobre pokracovanie.
Pockam trochu.
Potom zacneme tu druhu cast.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#27 19. 04. 2017 19:58 — Editoval vanok (19. 04. 2017 19:59)
Re: Osy, pomery
Ahoj akdar,
Co sa tyka vzorca z  , tak vyuzi ze plocha (ABC )=plocha (ABD)+plocha (ADC). A tiez pouzi klasicke vzozce ako
, tak vyuzi ze plocha (ABC )=plocha (ABD)+plocha (ADC). A tiez pouzi klasicke vzozce ako  atd.
atd.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#29 21. 04. 2017 23:21
Re: Osy, pomery
Dobry vecer ↑ akdar:,
Dobre si to upravila.
Ak ta este nieco zaujima o osach, tak to napis.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#31 26. 04. 2017 10:28
Re: Osy, pomery
Ahoj ↑ akdar:,
Dobre dnes budeme pokracovat ( Ak budem mat internet...)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#33 07. 05. 2017 23:55 — Editoval vanok (15. 05. 2017 00:35)
Re: Osy, pomery
Ako som slubil v #24 tu teraz definujem
pojem dvojpomeru
4roch bodov A, B, C, D tej istej priamky, je tento vyraz 
(Kde  je algebricka dlzka ...)
je algebricka dlzka ...)
Pomocou suradnic sa to da napisat takto .
.
Oznacime ho  .
.
Poznamka a cvicenie.
Cize 4 body A, B, C, D tvoria 24 dvojpomerov ak ich poprehadzujeme, napr.  .
.
Vyjadrite ich ak viete, ze  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#36 08. 05. 2017 01:08
Re: Osy, pomery
↑ akdar:
Dakujem
Bol tam preklep (opravil som)
Ak nepouzijes poschodovy zlomok tak pis inac zapis nema zmysel
inac zapis nema zmysel
Latex.... pouzi \frac
Vo vypoctoch vzdy treba respektovat poradie.
Je len 6 moznych hodnot
p, 1-p, 1-1/p, 1/p, 1/(1-p), 1/(1-1/p)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#37 08. 05. 2017 12:56 — Editoval vanok (08. 05. 2017 12:56)
Re: Osy, pomery
Dakujem
Bol tam preklep (opravil som)
Ak nepouzijes poschodovy zlomok tak pis inac zapis nema zmysel
inac zapis nema zmysel
Latex.... pouzi \frac {X}{Y}, kde X,Y su formy \frac {}{}.
Vo vypoctoch vzdy treba respektovat poradie. ( az na zatvorky mas to dobre)
Je len 6 moznych hodnot
p, 1-p, 1-1/p, 1/p, 1/(1-p), 1/(1-1/p)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#39 09. 05. 2017 00:12 — Editoval vanok (09. 05. 2017 00:12)
Re: Osy, pomery
Ahoj ↑ akdar:,
Co si myslis?
Mam hned pridat nejake zakladne vlasnosti dvojpomerov, alebo mam ist rychlejsie a pisat len o tom vo nam bude uzitocne vo vysetreni vlasnosti Apollonius-ovej kruznice.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#41 09. 05. 2017 21:34
Re: Osy, pomery
Dobre ↑ akdar:,
tak ukazeme najprv dve vlasnosti.
prva vlasnost
Je mozne najst dve usecky ktorych pomer je (ABCD)
druha vlasnost
Ak su dane 3 body A,B,C na jednej priamke, tak je mozne najst na nej bod D, taky, (ABCD)=r
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#42 10. 05. 2017 23:14
Re: Osy, pomery
Offline
#43 11. 05. 2017 23:32 — Editoval vanok (15. 05. 2017 00:31)
Re: Osy, pomery
Ahoj ↑ akdar:,
Tvoj navrh riesenia je dobry....
No stredoskolakom sa ukazalo, konstrukcne riesenie daneho pomeru, ci daneho bodu.
Prva vlasnost :
Nech A,B, C, D 4 body ( jednej priamky) a (ABCD) dvojpomer chceme representovat ako pomer dvoch useciek.
Konstrukcia.( obrazok nacrtnut )
Cez dva body A,B narysujme dve rovnobezky a, b.
Na priamke a zoberme jeden bod O a spojme ho z D a aj z C.
Nech priesecik OC a b je bod N
A priesecik OD a priamky b je bod M.
Vdaka podobnosti vhodnych trojuholnikov mame : 
Napiste podrobnosti dokazu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#44 12. 05. 2017 23:14
Re: Osy, pomery
Offline
#45 14. 05. 2017 17:46 — Editoval vanok (15. 05. 2017 00:38)
Re: Osy, pomery
↑ akdar:,
Ano presne tak ako si to pouzila, sa mohla pouzit podobnost trojuholnikov CAO a CBN, ako aj DAO a DBM.( poznamka :v dokaze treba pouzit  atd aby pouzite useky boli spravne orientovane)
atd aby pouzite useky boli spravne orientovane)
Druha vlasnost.
Dokaz.
Akoze by A, B, C su dane na jednej priamke d a chceme konstruhovat bod tak aby (ABCD)=r;
vedme cez A a C dvojicu rovnobeziek  a na
a na  narysujme repesentant jednotky
narysujme repesentant jednotky 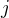 ako
ako ![kopírovat do textarea $[BJ]$](/mathtex/46/46a53187d6ff9b20ec8d6b77220aa0e6.gif) podla vybranej dlzky a z pociatkom v bode
podla vybranej dlzky a z pociatkom v bode  , podla znamienka
, podla znamienka  narysujme na tejto priamke aj representant
narysujme na tejto priamke aj representant  ako
ako ![kopírovat do textarea $[BK]$](/mathtex/73/737deddd571f7dd353eef8f4705e5748.gif) ( merany v jednodkou
( merany v jednodkou 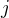 ) z pociatkom v
) z pociatkom v  a tak isto orientovany ako
a tak isto orientovany ako 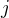 ak
ak  je kladne a opacne orentovany ak
je kladne a opacne orentovany ak  je negativne.
je negativne.
Priamka JB pretne  v bode O,
v bode O,
a priamka OK pretne priamku d v bode D. ( co je zarucene vdaka prvej vlasnosti )
Poznamka. Je dobre si nacrtnut popisanu situaciu.
V dokazoch sme predpokladali, ze dane body su rozne od seba, situaciu, ze by boli aj niektore z nich totozne nechame citatelom. ( vtedy  )
)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#46 15. 05. 2017 01:14 — Editoval vanok (16. 05. 2017 14:11)
Re: Osy, pomery
Ahoj ↑ akdar:,
Tak pokracujme.
Teraz definujme zväzok polopriamok : to je mnozina polopriamok ktore maju ten isty pociatok,
( poeticky kazdu z polopriamok zväzku volajme luc zväzku).
Tiez definujme dvojpomer zväzku 4roch lucov, ako dvojpomer 4roch bodov urcenych zväzkom na lubovolnej priamke ( transversale, priecke) ktoru pretina.
Posledna definicia je platna lebo mame
Teoremu 1.
Dvojpomer bodov prieseku jedneho zväzku 4roch polopriamok (zo spolocnym pociatkom) =lucov s lubovolnou priamkou je nezavisly od jej polohy.
Nacrtnut situaciu je uzitocne.
(Nostalgicka poznamka: Ze geometria co sa ucila pred 50timi rokmy na strednych skolach je celkom zabavna....)
Cakam na dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#47 15. 05. 2017 22:22
Re: Osy, pomery
Ahoj ↑ vanok:
tak jsem si to nakreslila, ale špatně, protože pokud ty příčné přímky nebudou rovnoběžné, tak ten dvojpoměr nebude stejný :-( Schválně jsem to i přepočítala numericky. Můžeš mi, prosím najít chybu.
Offline
#48 15. 05. 2017 22:36
Re: Osy, pomery
↑ vanok:
děkuji za upozornění na označení - vůbec mi ta orientace nedošla, měla jsem to na více papírech, tak aby se mi to dobře porovnávalo a hledalo, brala jsem to abecedně :-) (protože mě zajímá vzdálenost bodů a  tak mi to vůbec nepřišlo důležité)
tak mi to vůbec nepřišlo důležité)
Důkaz 2 si narýsuji zítra :-)
A ano, tahle geometrie je moc hezká :-)
Offline
#49 15. 05. 2017 23:33 — Editoval vanok (16. 05. 2017 07:46)
Re: Osy, pomery
↑ akdar:,
Dvojpomer je rovnaky (OPQR)=(IJKL). (Pretoze si v tom istom zväzku)
Over miery z tvojho obrazku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline




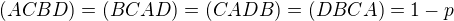




![[img]//forum.matweb.cz/upload3/img/2017-05/22335_PODOBNOST.png]([img]//forum.matweb.cz/upload3/img/2017-05/22335_PODOBNOST.png) [/img]
[/img]
