Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 05. 2017 13:34 — Editoval vlado_bb (16. 05. 2017 13:36)
Re: Ujasnění
↑ Cynyc: Ano, zastavam rovnaky nazor. Rovnost a nerovnost su relacie medzi prvkami toho isteho typu, teda rovnat alebo nerovnat sa moze cislo cislu, mnozina mnozine a podobne. Podla mna je napriklad zapis  nie nespravny, ale nezmyselny.
nie nespravny, ale nezmyselny.
Offline
#3 16. 05. 2017 16:22
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ vlado_bb:
Co to znamená "prvek stejného typu"? Zápis  je pravdivý výrok, protože
je pravdivý výrok, protože  i
i  jsou množiny a ty množiny se nerovnají...
jsou množiny a ty množiny se nerovnají...
Budoucnost patří aluminiu.
Offline
#4 16. 05. 2017 16:31
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Cynyc:
Ahoj, možná by se měl vyjádřit nějaký logik, myslím, že ve formální logice je znak  jen zkratkou za negaci
jen zkratkou za negaci  .
.
A pokud zavedeme "pravidlo", že vše je množina, pak má smysl porovnávat libovolné prvky...
Otázka je, co to ve formální logice zanmená, že nějaký výraz "nemá smysl". Např. "5/0" je syntaktický zápis nějakého výrazu, ale neodpovídá žádnému prvku v žádném modelu...
"Máte úhel beta." "No to nemám."
Offline
#5 16. 05. 2017 22:44
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ check_drummer:
:-)
No, nevím. Všechno množina asi být nemůže. Například p => q je výrok a zápisy typu (p')' = p by se obhajovaly asi težko...
Budoucnost patří aluminiu.
Offline
#6 16. 05. 2017 23:03
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Eratosthenes:
Dalo by to vyřešit tak, že sestrojíme třídy ekvivalence a do každé třídy umístíme ty "řetězce", které se rovnají (čistě formálně), takže p a (p')' budou ve stejné třídě. Musíme nejdřív zavést vhodný jazyk, tj. zde jazyk logiky obsahující symboly pro implikaci, ekvivalenci, apod.
"Máte úhel beta." "No to nemám."
Offline
#7 17. 05. 2017 16:08
Re: Ujasnění
Diskuse ujela malinko jinam, takže konkrétně: mám-li předpoklad  , znamená to podle Vás, že
, znamená to podle Vás, že  existuje a nerovná se nule, nebo nemusí ani existovat? Pokud je
existuje a nerovná se nule, nebo nemusí ani existovat? Pokud je  úplnou negací
úplnou negací  , je možné obojí, pokud je to relace a předpokládá smysluplnost obou stran, pak jen to první.
, je možné obojí, pokud je to relace a předpokládá smysluplnost obou stran, pak jen to první.
Offline
#8 17. 05. 2017 17:49
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Cynyc:
Ahoj, myslím, že se myslí, že musí existovat (nebo tak to často v textech bývá). Ale stejně je asi dobré to explicitně uvést.
"Máte úhel beta." "No to nemám."
Offline
#9 17. 05. 2017 18:52
Re: Ujasnění
Tiež sa prikláňam ku tomu, že vo výraze  by a aj b mali mať "zmysel" to ale podľa mňa nemusí znamenať že by mali existovať. Preto pre mňa je napríklad tvrdenie
by a aj b mali mať "zmysel" to ale podľa mňa nemusí znamenať že by mali existovať. Preto pre mňa je napríklad tvrdenie v reálnej analýze nezmyselné, ale tvrdenie
v reálnej analýze nezmyselné, ale tvrdenie  je OK.
je OK.
MATH IS THE BEST!!!
Offline
#10 19. 05. 2017 22:21
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
Myslím, že ty prvky musí existovat - jinak by neplatila taková tvrzení jako  , apod.
, apod.
"Máte úhel beta." "No to nemám."
Offline
#11 19. 05. 2017 22:45
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ check_drummer:
To tvrzení ale neplatí: Vezmi a=2+i; b=1+2i a máš po něm...
Budoucnost patří aluminiu.
Offline
#12 20. 05. 2017 00:10
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Eratosthenes:
beru to tak, že jsme v R, funkce z R do R a limity,integrály nad tím, šlo by to definovat induktivně.
Kdybychom byli v C, tak by to šlo změnit na 
"Máte úhel beta." "No to nemám."
Offline
#13 20. 05. 2017 10:17 — Editoval Eratosthenes (20. 05. 2017 20:20)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ check_drummer:
jenomže se bavíme o tom, zda při  musí a,b existovat. Jestli to bereš tak, jak říkáš, pak by tvoje tvrzení začínají
musí a,b existovat. Jestli to bereš tak, jak říkáš, pak by tvoje tvrzení začínají  , což znamená, že a;b, o kterých tvrdíš
, což znamená, že a;b, o kterých tvrdíš  , existují. Takže tvoje argumenty jsou podle mě mimo.
, existují. Takže tvoje argumenty jsou podle mě mimo.
Ani a ani b neexistuje, a přesto je to pravda.
PS: A aby té legrace nebylo málo, toto
je pravda taky :-)
Budoucnost patří aluminiu.
Offline
#14 20. 05. 2017 23:22
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Eratosthenes:
Tak jinak - pokud a,b neexistují a jde o totožné objekty (např. stejnou limitu), tak budeš psát  ? :-)
? :-)
"Máte úhel beta." "No to nemám."
Offline
#15 20. 05. 2017 23:54
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ check_drummer:

 jsem čínský bůh srandy
jsem čínský bůh srandy
Všechny tři výroky jsou pravdivé. Je-li totiž výrok A nepravdivý, je A => B vždycky pravdivé, a to zcela bez ohledu na pravdivost či nepravdivost výroku B. Najdeš to na třetí straně každé učebnice elementární logiky.
Budoucnost patří aluminiu.
Offline
#16 21. 05. 2017 02:03
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Eratosthenes:
Uniká mi souvislost s tím, co je předmětem tohoto vlákna.
"Máte úhel beta." "No to nemám."
Offline
#17 21. 05. 2017 09:55
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ check_drummer:
V tomto vlákně řešíme otázku, zda zápis  znamená, že a; b musejí existovat. Příspěvkem ↑ Eratosthenes: odpovídám, že ne.
znamená, že a; b musejí existovat. Příspěvkem ↑ Eratosthenes: odpovídám, že ne.
Budoucnost patří aluminiu.
Offline
#19 21. 05. 2017 12:08
#20 21. 05. 2017 12:15 — Editoval vlado_bb (21. 05. 2017 12:17)
Re: Ujasnění
↑ Eratosthenes: Nemam na mysli existanciu limity ale korektnost zapisu, lebo z predchadzajuceho vyplyva, ze napriklad zapis  z hladiska niektorych diskutujich nie je v poriadku.
z hladiska niektorych diskutujich nie je v poriadku.
Offline
#21 21. 05. 2017 12:41 — Editoval Eratosthenes (21. 05. 2017 12:41)
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ vlado_bb:
Ono z hledisla některých diskutujících je (bohužel) špatně například i řešení následujícího příkladu:
Určete limitu 
Řešení => limita neexistuje
=> limita neexistuje
V řešení totiž kladu rovnítko mezi neexistující čísla. Poradí mi odpůrci, jak jinak mám to řešení napsat?
Budoucnost patří aluminiu.
Offline
#22 21. 05. 2017 16:09
Re: Ujasnění
Poznamka,
Na taketo diskuzie treba urcit ramec v akom chcete pracovat.
Uzitocne ( ale nie kompletne ) citanie moze byt
https://en.m.wikipedia.org/wiki/Law_of_identity
Alebo aj
https://fr.m.wikipedia.org/wiki/Principe_d%27identité .
Inac asi kazdy bude o niecom inom hovorit! A vtedy je dialog nemozny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 21. 05. 2017 17:20
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Ujasnění
↑ vanok:
no, já nevím. Toto fórum je matematické a středověké filozofy bych do toho netahal. Jinak z toho tady taky může být diskuse na téma kolik andělů se vejde na špičku jehly...
Budoucnost patří aluminiu.
Offline
#24 21. 05. 2017 18:17 — Editoval vanok (21. 05. 2017 18:17)
Re: Ujasnění
Ahoj ↑ Eratosthenes:,
Tak sa mozes limitovat na formalnu logiku... ale pripadne, len na formalnu logiku propozicii.
Ale robit polo-filozoficke uvahy bez upresnenia pouzitych pojmov nemoze dat nic plodne.
Co sa tyka limit, ako tu ↑ Eratosthenes: formalne by bolo treba pokial existencia nejakej limity nie je dokazana, napisat, pred pouzitim rovnosti ak limita existuje, tak mame ....
No nebudem zbytocne polemizovat. V tejto diskuzii neplanujem pokracovat ... nemam na to cas.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 22. 05. 2017 16:04
- check_drummer

- Příspěvky: 4892
- Reputace: 105
Re: Ujasnění
↑ Eratosthenes:
Nepochopil jsem tu úvahu: Ty jsi dokázal, že  . To je jasné.
. To je jasné.
Ale jak to souvisí s tím, že pro neexistující a,b může platit 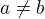 ?
?
"Máte úhel beta." "No to nemám."
Offline
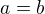 , neplatí i tehdy, když některá strana nemá smysl, ale zápis
, neplatí i tehdy, když některá strana nemá smysl, ale zápis 
 neexistuje."?
neexistuje."?