Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 22. 05. 2017 17:16 — Editoval Eratosthenes (22. 05. 2017 17:43)
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑↑ check_drummer:
Za prvé se vůbec nebavíme o tom, zda tvrzení a=b;  pro neexistující a, b platí nebo neplatí. Bavíme se o tom, zda zápisy a=b;
pro neexistující a, b platí nebo neplatí. Bavíme se o tom, zda zápisy a=b;  pro neexistující a, b mají smysl. A to je úplně a naprosto něco jiného.
pro neexistující a, b mají smysl. A to je úplně a naprosto něco jiného.
Za druhé - vycházím z implikací

Ty implikace jsou pravdivé, takže jejich atomické výroky  ;
;  určitě mají smysl.
určitě mají smysl.
A ptám se: existují taková a, b, aby platilo a=a+1; b=b-2?
Samozřejmě že ne.
A je to - a, b neexistují a zápisy  ;
;  mají smysl.
mají smysl. 
Ani jedna limita neexistuje a takových zápisů rovností limit, které neexistují, jsou plné učebnice.
Označ 


a, b, c neexistují, ale zápis a=b=c má smysl.
Budoucnost patří aluminiu.
Offline
#27 22. 05. 2017 19:29
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
Eratosthenes napsal(a):
Za prvé se vůbec nebavíme o tom, zda tvrzení a=b;
pro neexistující a, b platí nebo neplatí. Bavíme se o tom, zda zápisy a=b;
pro neexistující a, b mají smysl.
To právě ne, podle mě tazatel Cynic se v prvním příspěvku ptá, jak je to s platností toho výroku 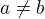 pro a,b která neexistují (nemají smysl). Ale ať mě případně opraví.
pro a,b která neexistují (nemají smysl). Ale ať mě případně opraví.
Jemu asi nejde jen o to, zda ten výrok má smysl, k čemu by mu to bylo? Jeho motivace je dle mého jeho platnost.
"Máte úhel beta." "No to nemám."
Offline
#28 23. 05. 2017 08:23
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ check_drummer:
Jak známo opět z elementární logiky, pro neexistující objekty může platit cokoliv. Takže pokud a,b neexistují, platí jak a=b, tak a<>b. Jak a=a, tak a<>a.
Budoucnost patří aluminiu.
Offline
#29 23. 05. 2017 15:22
#30 23. 05. 2017 16:50
Re: Ujasnění
Zdravím v diskusi. Já to vidím takto:
Nechť  je formule s volnou proměnnou
je formule s volnou proměnnou  . To znamená, že když do ní za
. To znamená, že když do ní za 
dosadíme nějakou konkretní konstantu  , nastane právě jeden z následujících "stavů":
, nastane právě jeden z následujících "stavů":
1. Vznikne smysluplný výrok  , který bude pravdivý a jehož negací bude
, který bude pravdivý a jehož negací bude
nepravdivý výrok  ,
,
2. Vznikne smysluplný výrok  , který bude nepravdivý a jehož negací bude
, který bude nepravdivý a jehož negací bude
pravdivý výrok  ,
,
3. Vzniklý tvar  nebude smysluplným výrokem (krátce řečeno: nebude výrokem),
nebude smysluplným výrokem (krátce řečeno: nebude výrokem),
a tudíž nebude výrokem ani tvar  .
.
Offline
#31 23. 05. 2017 17:24
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ check_drummer:
například 
nebo
nebo
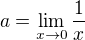
Možností je nekonečně mnoho
Budoucnost patří aluminiu.
Offline
#32 23. 05. 2017 17:33
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ Rumburak:
...jasně
A my se tady bavíme jenom o 1. a 2. S tím, že tvrdím:
Je-li A => B smysluplný výrok, jsou i A; B smysluplné výroky. A to my asi sotva někdo vyvrátí :-)
Takže tvrdím
je smysluplný výrok (dokonce pravdivý), takže i  je smysluplný výrok, i když a neexistuje.
je smysluplný výrok, i když a neexistuje.
Budoucnost patří aluminiu.
Offline
#33 23. 05. 2017 22:09
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ Eratosthenes:
Takže si dáme trošku hlubši úvahy z logiky:
1) Já jsem se ptal na definici nikoli na příklady, ale asi by šlo ten pojem "neexistujícího prvku" nějak rozumně definovat. Jen by to byl asi metapojem a nikoli pojem, protože by v sobě nejspíš obsahoval spojení "existuje výrok ...". Ale to je celkem podružné.
2) (podstatný bod) Ty jsi ale nedokázal, že  (ani jsi nedokázal Goldbachovu domněnku, pokud bychom ji položili místo
(ani jsi nedokázal Goldbachovu domněnku, pokud bychom ji položili místo  ), dokázal jsi pouze platnost implikace
), dokázal jsi pouze platnost implikace  . Abychom pochopili ten rozdíl, zkoumejme jak vypadají matematická tvrzení: Tvrzení říká, že platí nějaký výrok B za předpokladu A. Tedy chceme dokázat B (to je náš cíl) a můžeme k tomu využít platnost výroku A (předpoklad). Zpravidla se to provádí tak, že dokážeme implikaci
. Abychom pochopili ten rozdíl, zkoumejme jak vypadají matematická tvrzení: Tvrzení říká, že platí nějaký výrok B za předpokladu A. Tedy chceme dokázat B (to je náš cíl) a můžeme k tomu využít platnost výroku A (předpoklad). Zpravidla se to provádí tak, že dokážeme implikaci 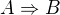 a pak díky tomu, že A platí odvodíme na základě pravidel logiky (jde o tzv. pravidlo modus ponens), že platí B. Podstatným krokem je důkaz oné implikace, ale konečným cílem není dokázat tu implikaci, ale B. Je to drobná nuance a při méně formálních důkazech není ani zřejmá, protože tyto důkazy probíhají tak, že "vyjdeme od platného tvrzení A a logickými důsledky dospějeme k B". Ale např. v našem případě, kdy A je nepravdivé tvrzení, je ten rozdíl zcela fatální. Únikem z toho je definovat tu neexistenci nějak pozitivně - jako nějaké platné tvrzení - např. jako, že "pro všechna x neplatí T". Z takové definice se nám ovšem vytvrátí onen "prvek" (to ale souvisí s dalším bodem).
a pak díky tomu, že A platí odvodíme na základě pravidel logiky (jde o tzv. pravidlo modus ponens), že platí B. Podstatným krokem je důkaz oné implikace, ale konečným cílem není dokázat tu implikaci, ale B. Je to drobná nuance a při méně formálních důkazech není ani zřejmá, protože tyto důkazy probíhají tak, že "vyjdeme od platného tvrzení A a logickými důsledky dospějeme k B". Ale např. v našem případě, kdy A je nepravdivé tvrzení, je ten rozdíl zcela fatální. Únikem z toho je definovat tu neexistenci nějak pozitivně - jako nějaké platné tvrzení - např. jako, že "pro všechna x neplatí T". Z takové definice se nám ovšem vytvrátí onen "prvek" (to ale souvisí s dalším bodem).
Poznámka: Pokud Ti to zdůvodnění s implikací nepřijde správné, tak ale trvám na tom, že je nutné danou vlastnost definovat nějak pozitivně, tj. jako nějaké tvrzení, které předpokládáme, že platí, pokud je daná vlastnost splněna.
3) Původní záměr tohoto vlákna se týkal konkrétních výrazů, o kterých chceme prohlásit, zda se (něčemu) rovnají nebo ne, tak definujme existenci nebo neexistenci takových výrazů. Např. si myslím, že by bylo možné definovat, že výraz v (to je právě nějaká konkrétní limita, apod.) existuje, právě když "existuje r takové, že r=v" (případně můžeme specifikovat i množinu, ze které r pochází, např. reálná čísla). A pak můžeme definovat, že v neexistuje právě když non(v existuje). A pomocí této ("pozitivní") definice již lze odvozovat další tvrzení týkající se výrazu v.
"Máte úhel beta." "No to nemám."
Offline
#34 24. 05. 2017 11:00 — Editoval jarrro (24. 05. 2017 11:10)
Re: Ujasnění
↑ check_drummer:Ahoj čo vravíš na definíciu:"Povieme, že objekt  neexistuje práve vtedy keď
neexistuje práve vtedy keď  " ?
" ?
Je to meta pojem? (Neviem. Naozaj sa pýtam)
MATH IS THE BEST!!!
Offline
#35 24. 05. 2017 15:57 — Editoval Rumburak (24. 05. 2017 15:59)
Re: Ujasnění
↑ jarrro:
Ahoj.
To je vtipný příklad.
Domnívám se, že dokud neexistuje konkretní definice (či jiná dohoda), co je to (objekt)  ,
,
je symbol  pouze proměnná a připadá mi, že dělat nad ní nějaké úvahy o existenci nemá
pouze proměnná a připadá mi, že dělat nad ní nějaké úvahy o existenci nemá
smysl.
Ale fundovaným logikem nejsem.
Offline
#36 24. 05. 2017 16:15
Re: Ujasnění
↑ Rumburak:Ahoj napríklad vo všeobecnej teórii množin je všetko trieda teda
"Povieme, že trieda  neexistuje práve vtedy, keď platí
neexistuje práve vtedy, keď platí 
Skôr by ma zaujímalo či taká formula nie je v spore s nejakou axiómou teórie tried resp. mimo logiky ako takej
MATH IS THE BEST!!!
Offline
#37 24. 05. 2017 19:12
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ Rumburak:
Ahoj, no ona je to pouze proměnná - ale s tím, že pro ni platí ta formule. Tím je dáno co to je. Ono obecně nemáš ani v teorii množin definováno co konkrétně je to množina - jen, že splňuje jisté axiomy.
"Máte úhel beta." "No to nemám."
Offline
#38 24. 05. 2017 19:14
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ jarrro:
Ahoj, definice je to zajímavá. Já jsem se chtěl zaměřit na ty "konkrétní neexistující objekty", jako např. ty limity, apod. Jinak to podle mě není meta-pojem protože je to definováno pomocí standardní formule logiky (prvního řádu).
"Máte úhel beta." "No to nemám."
Offline
#39 24. 05. 2017 22:13
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ check_drummer:
>> A jak definuješ neexistující objekt?
Existující ani neexistující objekt nelze definovat. To, že nějaký objekt existuje nebo neexistuje je věta, která se nedefinuje, ale dokazuje, anebo vyvrací.
Budoucnost patří aluminiu.
Offline
#40 24. 05. 2017 22:15
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ check_drummer:
>> Ty jsi ale nedokázal, že 
Ale já jsem to nedokazoval. Tady vůbec nejde o to, zda je to pravda nebo nepravda. Už jsem to jednou říkal zde:
↑ Eratosthenes:
Budoucnost patří aluminiu.
Offline
#41 25. 05. 2017 00:26
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ Eratosthenes:
Je potřeba definovat, co to znamená, že má nějaký výraz smysl.
"Máte úhel beta." "No to nemám."
Offline
#42 25. 05. 2017 17:27
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ check_drummer:
ale to definováno přece je. V každé teorii má smysl každá gramaticky správná formule. A co je to GSF je definováno vždy hned jako druhý bod hned za abecedou.
Budoucnost patří aluminiu.
Offline
#44 26. 05. 2017 10:24
Re: Ujasnění
↑ check_drummer:
Ahoj.
Pokud je v TM někde řečeno, že libovolná proměnná představuje vždy nějakou
(byť i blíže neurčenou) třídu a tedy nikoliv židli, na které právě sedím :-), pak
samozřejmě ano.
Offline
#45 26. 05. 2017 15:52
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ Eratosthenes:
k čemu pak Tvůj "složitý" důkaz? Měl jsi proměnnou  a pro ni je
a pro ni je  gramaticky správná formule a tudíž dle definice má smysl.
gramaticky správná formule a tudíž dle definice má smysl.
"Máte úhel beta." "No to nemám."
Offline
#46 26. 05. 2017 15:54
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ jarrro:
Ale proměnné neoznačují vlastní třídy, jen "řádné" množiny.
"Máte úhel beta." "No to nemám."
Offline
#47 27. 05. 2017 11:59
Offline
#48 27. 05. 2017 12:28
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ jarrro:
Já bych řekl, že ano - možná z axiomu dvojice, k množině a existuje množina b tvaru {a,a} (nebo třeba {a,0}), tj. dvojice - to je ten axiom dvojice. no a je vidět, že b splňuje Tvé tvrzení.
"Máte úhel beta." "No to nemám."
Offline
#49 27. 05. 2017 12:30
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Ujasnění
↑ Eratosthenes:
Ještě mě napadlo, že z Tvé arumentace by plynulo, že "a=a+1 => a je pěkně vybarvená proměnná" a tedy že "a je pěkně vybarvená proměnná" má smysl. (Nebo chceme-li používat jen konkrétní symboly jazyka, tak třeba volme výrok "a=====a".)
"Máte úhel beta." "No to nemám."
Offline
#50 27. 05. 2017 19:13
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Ujasnění
↑ check_drummer:
ani
"a je pěkně vybarvená proměnná"
ani
"a=====a"
nejsou gramaticky správné formule, takže smysl nemají.
Budoucnost patří aluminiu.
Offline

