Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 01. 2008 21:31
Re: uprava vyrazu s odmocninami
Pro Sergej : našla jsem chybu ,posílám řešení v odkazu.Provedla jsem si i zkoušku a vyšla mi. :-)
odkaz : http://matematika.havrlant.net/forum/up … G_0007.jpg
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#5 07. 01. 2008 06:57
Re: uprava vyrazu s odmocninami
@ Sergej a thriller : Ano, vidím svoji chybu :-( při konečném vytýkání . Děkuji za opravu.
posílám dokončení řešení. :-) Ahoj Ivana.
http://matematika.havrlant.net/forum/upload/466-IMG.jpg(/img)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#6 07. 01. 2008 09:25
- Ivana Hnátková
- Zelenáč

- Příspěvky: 22
- Reputace: 0
Re: uprava vyrazu s odmocninami
Posílám zkoušku pro ... a=4 1-8 1+8
(----- + 2)*(------- -2) = (7+2)*(3-2)= 9 ...... do zadání
-1 3
(4-1)^2 = 3^2 = 9 ...... do výsledku >>> zkouška vyšla
Ve fyzice není tak důležité tvrzení, jako vědět, proč tomu tak je.
Offline
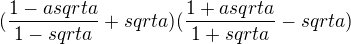

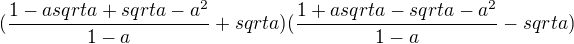

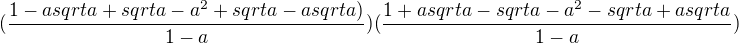
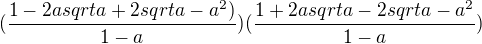
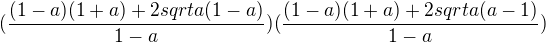
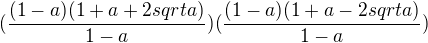

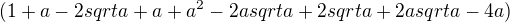
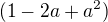


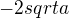

![kopírovat do textarea $(\frac{1-a sqrt a}{1- sqrt a}+sqrt a)(\frac{1+a sqrt a}{1+ sqrt a}-sqrt a) = \frac{[(1-a) + \sqrt{a} (1-a)].[(1-a) - \sqrt{a} (1-a)]}{1-a} = (1-a)^2 $](/mathtex/cd/cd58460b4aa41fdc6181e208bb44ef0c.gif)