Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 08. 2017 12:21
Hodnost matice
Mějme matici A, určete hodnost matici v závislosti na parametru 

Potřeboval bych návod jak toto vyřešit, jednu lehči rovnici s parametrem se mi podařilo vyřešit, ale tady jsem se dostal do problemů.
Začal bych zaměnou 1. a 3. řádku
Pak, potřebuji dostat po hlavni diagonálou 0, ale tam pravě se dostavam do problému,a nevím jak dál.
Děkuji za reakci :)
Offline
- (téma jako vyřešené označil(a) byk7)
#2 07. 08. 2017 12:31 — Editoval Rumburak (07. 08. 2017 14:50)
Re: Hodnost matice
↑ Davisek:
Ahoj.
Do jakých problémů ses dostal ?
EDIT. Snad tuším. Máme tedy matici
 .
.
Pořadí řádlků zatím ponechme, jak je, a první řádek odečtěme od druhého. Dostaneme matici

mající tutéž hodnost jako matice  .
.
Nyní v matici 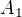 odečtěme
odečtěme  - násobek prvního řádku od třetího řádku. Vznikne matice
- násobek prvního řádku od třetího řádku. Vznikne matice

opět téže hodnosti.
V matici 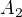 přičtěme druhý řádek ke třetímu . Vznikne matice
přičtěme druhý řádek ke třetímu . Vznikne matice

téže hodnosti. Z matice 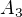 ji určíme snadno (v závislosti na
ji určíme snadno (v závislosti na  ), pokud víme,
), pokud víme,
o čem je řeč.
EDIT 2 . V kroku vedoucím k matici 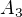 jsem ještě opravil numerickou chybu,
jsem ještě opravil numerickou chybu,
za niž se omlouvám.
Offline
#4 07. 08. 2017 13:04 — Editoval Ferdish (07. 08. 2017 13:06)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Hodnost matice
↑ Davisek:Už tú prvú maticu si "pomixoval" s tou, kde si vymenil 1. a 3. riadok.
Kolega ↑ Rumburak: ti v edite ukázal, ako na to.
Offline
 a přičetl ke druhemu
a přičetl ke druhemu
 a přičetl jsem ke 3.
a přičetl jsem ke 3.