Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 03. 10. 2017 15:27
Re: Goniometrie
takhle to mám, potom jsem použila vzorec pro sin 2beta+ sin 2 gamma, pak jsem po úpravě dosadila za beta + gamma = 180- alfa , něco se mi vynulovalo, potom jsem použila vzorec pro sin 2alfa, vytkla a pak vykrátila sin alfa, zbylo mi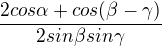
pak jsem dosadila za alfa = 180-(beta+gamma) , něco se vynulovalo a zbylo mi
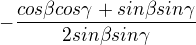
možná je to zbytečně dlouhý
Offline
#8 03. 10. 2017 16:12
Re: Goniometrie
↑ aniuce:
budu psát pouze čitatele, začal jsem nejprve podle tvého: " použila jsem vzorec pro sin 2beta+ sin 2 gamma" a využívám skutečnost, že 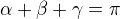
Offline


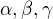 ? Třeba, že je jejich součet roven
? Třeba, že je jejich součet roven 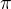 ?
?