Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 10. 2017 15:02 — Editoval Akraell (29. 10. 2017 15:03)
Lineární závislost polynomu
Zdravím,
Mám tu 5 prvků a chci ověřit lineární nezávislost. Udělal jsem z toho matici, kde se snažím vynulovat v poslední řádce 5 čísel. Jenže dostal jsem akorát 2 papíry přeplněné úpravami jedné matice. Pak jsem zjistil ve výsledku, že p5 má být úplně vyřazen, takže poslední řádka by měla být asi úplně vynulovaná. Po snaze to vynulovat celý jsem akorát dostal další kotel matic po úpravě té jedné. Poradíte mi prosím strategii?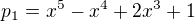

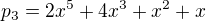

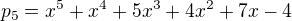
Offline
#2 29. 10. 2017 16:44
Re: Lineární závislost polynomu
Ahoj ↑ Akraell:,
To mas pravdu, ze mozes povazovat tvoje  ako vektory.
ako vektory.
Akeho priestoru?
Ak pracujes z maticami mozes vysetrit hodnost nejakej vhodnej matrice. Aku by si pouzil?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 29. 10. 2017 21:56
Re: Lineární závislost polynomu
Matica je typu 6x5
Staci pouzit GEM a sa pokusit ju « triangolizovat »
( co som nerobil ) ak po skonceni metody mas vsetki riadky nenulove tak tvoje polynomy su LN.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 29. 10. 2017 22:42
Re: Lineární závislost polynomu
Gaussovu eliminační metodu používám už od samého začátku. Teprve před třemi hodinami jsem ji řešil s lepší strategií, že číslem prvního sloupce prvního řádku vynuluji ostatní čísla v prvním sloupci a postupně tvořím trojúhelník. Jenže mi na posledním řádku zůstanou dvě nenulová čísla. Na stránce s výsledky jsem nalezl, že pátý prvek má být vyloučen, takže pátá řádka matice by měla být LZ a zcela vynulovaná. Jenže nejsem schopný toho dosáhnout.
Offline
#6 30. 10. 2017 00:02 — Editoval vanok (30. 10. 2017 00:04)
Re: Lineární závislost polynomu
Cize pouzivas dobru metodu. Dufam, ze najdes kde si sa zmylil.
Inac napiis cely postup a potom skusim najst kde je chyba.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 30. 10. 2017 19:54
Re: Lineární závislost polynomu
↑ Akraell:,
Vyborne
Vela uspechov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
