Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet osi medzi dvoma priamkami (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 11. 2017 19:15
Výpočet osi medzi dvoma priamkami
Ahoj,mám parametricky zadané 2 priamky :![kopírovat do textarea $p: [3,0,3] + t(0,1,2)$](/mathtex/30/30317d0174f21637beeeb8d9e81d8a99.gif)
![kopírovat do textarea $q: [0,-1,-2]+s(1,2,3)$](/mathtex/2d/2dfaa8f1316b3400f16aea9b9e66ce67.gif)
Vieme,že os je kolmá na obe priamky,takže som si vyrátal vektor,ktorý je kolmý na vektory 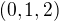 a
a  .. dostal som vektor
.. dostal som vektor 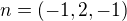
Takže 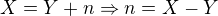 ,kde
,kde 
Ďalej som postupoval takto: Bod X musí vyhovovať ![kopírovat do textarea $[3,0,3] + t(0,1,2)$](/mathtex/d4/d4357ce3f43c63f520344b7f32b8b6ec.gif) a bod Y
a bod Y ![kopírovat do textarea $[0,-1,-2]+s(1,2,3)$](/mathtex/72/723f9cdde4d2b1414ae65a40f67c9bd6.gif) ,preto som si to prepisal ako
,preto som si to prepisal ako ![kopírovat do textarea $n = [3,0,3] + t(0,1,2) - [0,-1,-2] - s(1,2,3) = [3,1,5] + t(0,1,2)-s(1,2,3) \Rightarrow X = [3,1,5] $](/mathtex/1f/1ff57bb9a86ec3e6f60ee73e391a7b00.gif)
Podľa rovnice vyššie dostávame: ![kopírovat do textarea $Y = X - n = [3,1,5] - (-1,2,-1) = [4,-1,6]$](/mathtex/cd/cd2fd2b7d50838b443f0eefc35de6ef3.gif) ,avšak tento výsledok podľa riešení nie je správny,keby však prehodíme X a Y :
,avšak tento výsledok podľa riešení nie je správny,keby však prehodíme X a Y : ![kopírovat do textarea $X = Y - n \Rightarrow Y = X + n = [3,1,5] + (-1,2,-1) = [2,3,4]$](/mathtex/ab/abfccdbe73fc89b74aec58cf8eca028f.gif) , tak to už je správne riešenie ... vedel by mi niekto vysvetliť prečo? Ďakujem :-)
, tak to už je správne riešenie ... vedel by mi niekto vysvetliť prečo? Ďakujem :-)
Offline
- (téma jako vyřešené označil(a) sliziky)
#2 21. 11. 2017 19:47
Re: Výpočet osi medzi dvoma priamkami
Mám pocit ,že to záleží od normaloveho vektoru.Pokiaľ by bol v tvare (1,-2,1), tak potom by Y vyšiel správne aj z prvej rovnice. Stále však nechápem že ako to ovplyvní riešenie. Prečo by v tomto prípade musel byť použitý práve normalovy vektor v tvare(1,-2,1) a nie (-1,2,-1) ?
Offline
#3 21. 11. 2017 19:53 — Editoval misaH (21. 11. 2017 19:56)
- misaH
- Příspěvky: 13459
Re: Výpočet osi medzi dvoma priamkami
↑ sliziky:
X má byť z p, Y má byť z q a ich rozdiel má byť zistený vektor n.
Je to tak alebo nie je?
Offline
#5 21. 11. 2017 20:14
Re: Výpočet osi medzi dvoma priamkami
Ahoj ↑ sliziky:,
Ak chces hladat osu tvojich priamok tak sa musia pretinat.
Maju spolocny bod?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 21. 11. 2017 20:27 — Editoval vanok (22. 11. 2017 08:54)
Re: Výpočet osi medzi dvoma priamkami
↑ sliziky:,
Cize chces najst ich minimalnu vzdialenost?
Alebo rovnicu priamky ktora je ich spolocna kolmica?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 21. 11. 2017 20:28 — Editoval misaH (21. 11. 2017 20:33)
- misaH
- Příspěvky: 13459
Re: Výpočet osi medzi dvoma priamkami
↑ sliziky:
No.
Tušímže:
Keď si presne predstavíš o čo ide, tak rozdiel tých bodov môže byť (a asi aj musí) nenulový násobok toho vektora n.
Lebo tie body sú na tých priamkach jediné...
Offline
#10 21. 11. 2017 20:49 — Editoval misaH (21. 11. 2017 20:54)
- misaH
- Příspěvky: 13459
Re: Výpočet osi medzi dvoma priamkami
↑ sliziky:
Podľa Tvojich otázok Ti to jasné nie je... :-)![kopírovat do textarea $[3;0;3]+t(0;1;2)-[0;-1;-2]-s(1;2;3)=k(-1;2;-1)$](/mathtex/1b/1bc202c7090ef82cbb5fb68ecb46eb64.gif)
Rozpísať po zložkách, doriešiť...
Vyšlo mi:
Offline
#13 21. 11. 2017 21:40 — Editoval vanok (21. 11. 2017 21:51)
Re: Výpočet osi medzi dvoma priamkami
↑ sliziky:,
Dobre ked je mi teraz jasne, ze nehladas osu priamok, ktora neexistuje.(a neviem co volas osa)
Tak ti mozem navrhnut jednoduchu metodu ako nast spolocnu kolmicu dvom danym priamkam.
Oznacme body priamky p ako 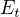 à body priamky q ako
à body priamky q ako 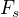 .
.
Priamka 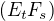 ma smerovy vektor (ten nie je jeznoznacne dany ...ake su jeho vlasnosti)
ma smerovy vektor (ten nie je jeznoznacne dany ...ake su jeho vlasnosti) 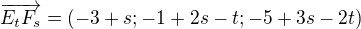
Oznacme smerove vektory priamky p, 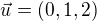 a smerovy vektor q
a smerovy vektor q 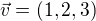
Nas ciel je najst take t,s aby priamka 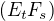 bola kolma z p a q.
bola kolma z p a q.
Napis mi ako znacite skalarny sucin a potom ti napisem ako sa da doriesit tvoje cvicenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 21. 11. 2017 21:57
Re: Výpočet osi medzi dvoma priamkami
Dobre, tak najprv treba vyriesit tento system

Dokazes to?
( tie skalarne suciny su= 0 pre tu kolmost).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 21. 11. 2017 22:19
Re: Výpočet osi medzi dvoma priamkami
Mala pomoc:
Prva rovnica sa pise 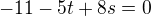
A druha....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 21. 11. 2017 22:44
Re: Výpočet osi medzi dvoma priamkami
Dobre. Ake si nasiel t, s?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 22. 11. 2017 10:21
Re: Výpočet osi medzi dvoma priamkami
↑ sliziky:,
Vyborne, tato metoda sa mi zda najkratcia.
A lahko sa vysvetluje.
Tak dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Výpočet osi medzi dvoma priamkami (TOTO TÉMA JE VYŘEŠENÉ)

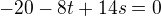 po úpravach som dostal dve rovnice o dvoch neznámych:
po úpravach som dostal dve rovnice o dvoch neznámych: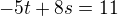
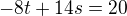
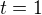 ,
, 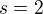
![kopírovat do textarea $X=[3,0,3] + 1(0,1,2) = [3,1,5]$](/mathtex/4c/4c7acee7bc5855a27414b9ebdd6d0ca5.gif)
![kopírovat do textarea $Y = [0,-1,-2]+2(1,2,3)=[2,3,4]$](/mathtex/47/479b3f85a89cbbc708c42bfa2986a3e4.gif)