Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyšetřete lokální extrémy fce n proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 01. 2018 18:22
- dominiksep
- Příspěvky: 54
- Reputace: 0
Vyšetřete lokální extrémy fce n proměnných
Ahoj,
potřeboval bych poradit s následujícím přikladem:
Vyšetřete lokální extrémy funkce uvnitř jejího definičního oboru, 
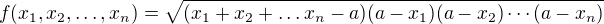
Zasekl jsem se už u toho, jak určit stacionární body. Vím, že se to nejlépe řeší, když si to člověk zapíše do sum a produktů, mám tedy:
Parciální derivace podle i-té proměnné - počítám jako derivaci součinu: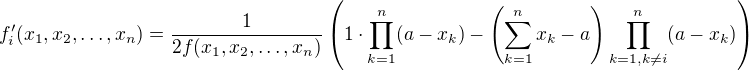
Zároveň chci 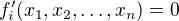
takže mám soustavu n rovnic pro n neznámých. První otázka bude asi znít, jak ji vyřešit?
Díky
Offline
- (téma jako vyřešené označil(a) dominiksep)
#2 16. 01. 2018 20:56
Re: Vyšetřete lokální extrémy fce n proměnných
↑ dominiksep:
Pouze v krátkosti první pozorování, které může pomoci. V poslední závorce uvedené v první derivaci vytkni druhý "méně obsažný" součin. Výraz vzniklý po vytknutí zjednoduš a ze součinového tvaru derivace vyloučením okrajových nulových bodů najdi jednodušší soustavu, z níž dostaneš odpovídající stacionární body.
Věřím, že kolegové se jistě připojí...
Offline
#3 17. 01. 2018 17:18
Re: Vyšetřete lokální extrémy fce n proměnných
↑ dominiksep:
Mám takový pocit, že se snažíš dvojnásobně (ale doufám, že se pletu), viz zde.
Ovšem uvedený příspěvek od @Michael Rozenberg neodpovídá na dotaz v tamním příspěvku. Dostat stacionární bod (bude jediný) je v tomto případě relativně jednoduché. O trochu horší je zjistit, že v takovém bodě je lokální maximum, ale nemožné to není...
Offline
#4 17. 01. 2018 22:28
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Vyšetřete lokální extrémy fce n proměnných
↑ Marian:
No, ono nás to řeší víc, kámoš má radši Math Stack :-D . Jinak jo, našel sice maximum a minimum, ale můžou tam být i další extrémy a ještě k tomu tam není uvedeno, v kterých bodech...
Jinak podle Tvého postupu mi vyjde: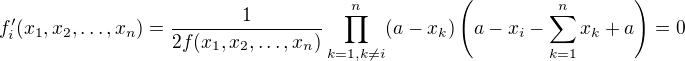
což je pravda buď pro 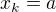 nebo
nebo 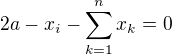
Ale jak s tím naložit dál. Je jasné, že první ze dvou řešení, tedy všechna x rovna a, je uvnitř definičního oboru a je to právě to minimum, o kterém se tam mluví. Ale co s tím druhým výrazem? Opět dostávám soustavu n rovnic, ale jak ji upravit dál, abych dostal výsledek. Něco mi říká, že kdybych to nějak pěkně posčítal, tak by se mi mohlo něco vymlátit.
Offline
#5 18. 01. 2018 09:29 — Editoval Marian (18. 01. 2018 09:30)
Re: Vyšetřete lokální extrémy fce n proměnných
↑ dominiksep:
x_k = a vyloučíme kvůli jejímu výskytu na okraji definičního oboru. Navíc tam funkce nabývá globálního minima.
Co se týče rovnic n rovnic, které uvádíš, dostaneš soustavu tvaru
2x_1 + x_2 + ... + x_n = 2a,
x_1 + 2x_2 + ... + x_n = 2a,
......................................
x_1 + x_2 + ... + 2x_n = 2a.
Prvky matice soustavy A = (a_ij) mají tvar a_ij = 1+delta_ij, kde delta_ij značí Kroneckerovo delta. Úpravou rozšířené matice soustavy na Gaußův stupňový tvar se dostaneš k jejímu řešení
x_1 = x_2 = ... = x_n = DOPLŇ
Dále budeš muset vypočítat druhé parciální derivace a vyšetřit existenci a povahu lokálního extrému v bodě x_0 = (x_1, x_2, ..., x_n).
Poznámka: Doporučuji přeskočit triviální případ n = 1, ve kterém nemá smysl hledat lokální extrém.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyšetřete lokální extrémy fce n proměnných (TOTO TÉMA JE VYŘEŠENÉ)
