Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 28. 02. 2018 19:05
Re: rozdělení čísel
↑ gadgetka: díky za lekci z češtiny, ale tato rada byla naprosto zbytečná
Offline
#5 28. 02. 2018 19:39
Re: rozdělení čísel
↑ MichalAld: to ne, samozřejmě vím , že největší součin je , když dané číslo rozdělím na dvě poloviny, např 10 = 5+5 a 5x5 = 25 což je nejvyšší možný výsledek. Mě zajímalo , zda to lze vyjádřit nějakým
matematickým výrazem např. 10 = x+y atd...
Offline
#7 28. 02. 2018 20:48
Re: rozdělení čísel
wendys napsal(a):
↑ gadgetka: díky za lekci z češtiny, ale tato rada byla naprosto zbytečná
Promiň, pochopila jsem tvůj dotaz jinak... :D
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#8 28. 02. 2018 22:21
Re: rozdělení čísel
Pozdravujem ↑ vlado_bb:,
Maly doplnok. Ak oznacim dane cislo M, potom hladany sucin je  .
.
Poznamka 1. Dane cvicenie nie je dost presne formulovane.
O ake cisla ide? Prirodzene? Cele? Realne? Kladne?
Poznamka 2. V kazdom pripade toto cvicenie sa da riesit bez pouzitia derivacii. ( a pozor v roznych situaciach, cvicenie nemusi mat to iste riesenie).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 01. 03. 2018 08:49
Re: rozdělení čísel
Ahoj ↑ Honzc:,
To je pekna a zaujimava uloha (pre stredoskolaka).
Uz aj zacat napr. s cislom 30 moze byt zaujimava aktivita.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 02. 03. 2018 01:00
Re: rozdělení čísel
Pozdravujem.
Poznamka.
Vratim sa este k ↑ wendys: v pripade ked chceme rozdelit dane kladne realne cislo M na dve casti take ze ich sucin je maximalny.
Vtedy ak nechceme pouzit derivacie na ich hladanie mozme pouzit, ze pre
pre ![kopírovat do textarea $ a \in [0;\frac M2]$](/mathtex/f1/f12502160ba75f8c7111e3668667f588.gif) .
.
A tato stara ( zabudnuta stredoskolska) veta nam to moze pripomenut
Sucin dvoch casti kladneho cisla M je maximalny ak tie dve casti su rovnake
.
Kto pozna este ine podobne zabudnute pekne vety? Poucte nas.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 02. 03. 2018 10:03
Re: rozdělení čísel
Honzc napsal(a):
↑ wendys:
To je sice hezké,(jednoduché) ale co tato úloha:
Jak rozdělit přirozené číslo n (n>3) na libovolný počet přirozených sčítanců n = a1 + a2 + ... + ak tak, aby jejich součin pmax = a1 . a2 ... ak byl co největší? Dokažte!
Nebo taky: jak rozdělit přirozené číslo n na součin dvou jiných čísel (a1 * a2), a aby nám to netrvalo moc dlouho...
Offline
#13 02. 03. 2018 10:10
Re: rozdělení čísel
vanok napsal(a):
Kto pozna este ine podobne zabudnute pekne vety? Poucte nas.
No já nevím, ale přijde mi, že na tenhle příklad je nejjednodušší si prostě napsat, jak jsi to udělal, že .
.
Takže vidíme, že je to parabola, a osu x protíná v bodech 0 a M. Kdo to nevidí, může si ji nakonec nakreslit.
Takže vrchol by měla mít v půlce, mezi body 0 a M.
Offline
#14 02. 03. 2018 10:31 — Editoval vanok (02. 03. 2018 10:32)
Re: rozdělení čísel
Ahoj ↑ MichalAld:,
To moze pomoct. Ale v matematike uz aj na SS sa cakaju dokazy. 😫
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 02. 03. 2018 11:02
#17 02. 03. 2018 12:29
Re: rozdělení čísel
↑ vlado_bb:
Tak to je jednodušší, než jsem čekal.
Dokázat, že x-ová poloha vrcholu leží v polovině průsečíků paraboly s osou x (nebo nějakou rovnoběžkou s osou x) už bude taky snadné.
Ale měl jsem za to, že je to všeobecně známá věc, že parabola je symetrická dle svislé přímky procházející vrcholem (parabola ve tvaru  samozřemě, nemyslím nějakou "natočenou")
samozřemě, nemyslím nějakou "natočenou")
Offline
#18 03. 03. 2018 03:25 — Editoval vanok (03. 03. 2018 10:48)
Re: rozdělení čísel
Ahoj ↑ MichalAld:,
Znovu si v situaci kde treba dokazat vyroky ktore povazujes za platne bez dokazov.
Matematika ma svoje pravidla. Mozes sa o tom poucit ked si prestudujes prace o fondaciach matematiky.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 03. 03. 2018 11:38 — Editoval MichalAld (03. 03. 2018 12:00)
Re: rozdělení čísel
↑ vanok:
Proč, stačí že to dokázali jiní přede mnou....(to bych s takovou za chvíli mohl při hledání řešení kvadratické rovnice dokazovat i základní větu algebry)
Ale když už to musí být, dokázat symetrii podle svislé osy u funkce  je dokázat, že
je dokázat, že  což zjevně platí,
což zjevně platí,
a u paraboly která není posazená na ose y je to dokázat, že
což zjevně platí taky.
Pořád mi to tak nějak přijde, že je to dokazování toho, že 1+1=2, (přesně tedy že 1*1=(-1)*(-1))
Navíc předpokládám, že když člověk místo koukání do mobilu si v hodině vyslechne, jaké že to má parabola vlastnosti, tak ty informace pak může při řešení úloh využívat, a nemusí je v každém příkladě znovu dokazovat. Že je levá a pravá strana kruhu stejná jsem taky nikdy nemusel dokazovat....
Offline
#20 03. 03. 2018 16:11
Re: rozdělení čísel
Ahoj ↑ MichalAld:,
To je ina diskuzia.
Zaloz na taketo veci ine vlakno.
Taketo uvahy nepis do vlakien ktore maju iny ucel.
Pre citatelov je potom z toho cakana odpoved nezrozumitelna.
Dakujem za porozumenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 03. 03. 2018 16:48
- misaH
- Příspěvky: 13459
Re: rozdělení čísel
↑ vanok:
Ahoj vanok.
Práveže Ty stredoškolskú problematiku zrejme vôbec nepoznáš. Tým, že neustále poukazuješ na veci (verím, že odborne pravdivé, ibaže mimo SŠ), ktoré s matematikou preberanou na SŠ nemajú nič, zahmlievaš témy.
(Proste nemôžeš s desaťročným človekom rozprávať rovnako ako s dvadsaťročným. Lenže Ty tomu nejako nedokážeš porozumieť...)
Tipujem, že kolega chcel (možno nepriamo) poukázať práve na to.
Offline
#22 03. 03. 2018 17:03 — Editoval vanok (03. 03. 2018 17:11)
Re: rozdělení čísel
Ahoj↑ misaH: ,
Ty si asi jasnovidkena.
Povedz mi moju buducnost a co si teraz myslim.
Desatrocne deti chodia na strednu skolu? Naozaj?
Tvoj postoj je pravidelne kritizovat ludi co ta raz upozornili na tvoje chyby. Ak si nepochopila co pisem tak aspon sa nehraj na pani ucitelku. Ty co vsetko rozumies.
No v kazdom pripade si sa dodnes nenaucila co je slusnost. Pracuj na sebe.
Vsetko krasne a prestan byt agresivna. Dakujem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 03. 03. 2018 22:15 — Editoval Peter_CSR (03. 03. 2018 22:20)
Re: rozdělení čísel
vanok napsal(a):
Pozdravujem ↑ vlado_bb:,
Maly doplnok. Ak oznacim dane cislo M, potom hladany sucin je.
Poznamka 1. Dane cvicenie nie je dost presne formulovane.
O ake cisla ide? Prirodzene? Cele? Realne? Kladne?
Poznamka 2. V kazdom pripade toto cvicenie sa da riesit bez pouzitia derivacii. ( a pozor v roznych situaciach, cvicenie nemusi mat to iste riesenie).
Troška prr páni :)
1) rád by som sa spýtal na význam  . Dalo by sa to preformulovať? Nejak som neporozumel...
. Dalo by sa to preformulovať? Nejak som neporozumel...
2) ako by sa zmenilo riešenie, keby to teda boli napr. prirodzené čísla?
prepodkladám že
wendys napsal(a):
lze matematicky zapsat : rozdělte číslo na dvě, aby jejich součin byl co největší
je  ,
,  ,
,  ,
, 
je odpoveď na OP otázku...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#24 03. 03. 2018 23:49
Re: rozdělení čísel
↑ Peter_CSR:
Ahoj.
Tu mas male vysvetlenie ktore ti moze trochu pomoct.
V predoslych prispevkoch som ukazal ze ak hladame maximalny sucin xy pre realne cislo M=x+y, tak vtedy x=y=M/2 vyhovuje.
Napisem ti dva priklady.
Ak M=20, tak x=y=10 da maximalny sucin xy=100 v realnom pripade a akoze tie x,y su prirodzene tak je to riesenie aj v prirodzenych cislach.
Ak M=21, x=y=10,5; to je riesenie v realnych cislach. Vtedy maximalny réalny y sucin je xy=110,25 ale to nie su prirodzene cisla.
Ak chces ma v tomto pripadne mat riesenie pre prirodzene cisla x, y take ze 21= x+y su prirodzene cisla, take ze mas maximalny sucin xy musis hladat inac.
A to nie je take jednoduche ako to bolo v predoslom pripade.
Najdes, ze x=10, x=11 ma sucin je xy=110 a to skutocne je maximalny sucin v prirodzenych cislach. ( to hladanie ti necham)
Tieto dva priklady ti ukazuju, ze probleme v pripade realnych cisiel je lahky, ale v pripade prirodzenych cisiel je to trochu zlozitejsie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


 je
je  , sucin zasa
, sucin zasa 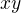 . V tomto pripade ide o maximum funkcie
. V tomto pripade ide o maximum funkcie  má vrchol (minimum) v bodě 0, tak ani nevím, jak bych to dělal (bez derivování).
má vrchol (minimum) v bodě 0, tak ani nevím, jak bych to dělal (bez derivování). a ak
a ak  , tak
, tak  . Teda
. Teda  je minimum funkcie
je minimum funkcie