Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lagrangeova věta - průběh funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 03. 2018 12:47 — Editoval BobMarley (13. 03. 2018 13:51)
Lagrangeova věta - průběh funkce
Dobrý den,
chtěl bych požádat o konzultaci nad tímto důkazem:
Má-li funkce  v každém bodě intervalu
v každém bodě intervalu 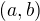 kladnou derivaci, je v tomto intervalu rostoucí.
kladnou derivaci, je v tomto intervalu rostoucí.
Našel jsem tento důkaz, který využívá Langrageovu větu o střední hodnotě:
Jsou-li  dva libovolné různé body intervalu
dva libovolné různé body intervalu 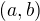 , pro která platí
, pro která platí  , je interval
, je interval  části intervalu
části intervalu 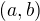 .
.
Podle Lagrangeovy věty existuje takové číslo  , že platí
, že platí .
.
Víme (z předpokladu), že  . Protože
. Protože  , musí být
, musí být  . Tím jsme dokázali, že pro
. Tím jsme dokázali, že pro 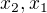 z intervalu
z intervalu 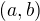 platí, je-li
platí, je-li  , je
, je  . To však znamená, že funkce
. To však znamená, že funkce  je rostoucí v
je rostoucí v 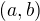 .
.
Poslední věta mi není jasná, nemělo by v důkazu spíše být uvedeno, že musí existovat podinterval intervalu  , ve kterém musí být funkce
, ve kterém musí být funkce  rostoucí? Protože definice rostoucí funkce vypadá přeci takto:
rostoucí? Protože definice rostoucí funkce vypadá přeci takto:  , což nemusí být přeci splněno.
, což nemusí být přeci splněno.
Offline
- (téma jako vyřešené označil(a) BobMarley)
#2 13. 03. 2018 13:43 — Editoval Rumburak (13. 03. 2018 13:44)
Re: Lagrangeova věta - průběh funkce
↑ BobMarley:
Ahoj.
Důkaz je v pořádku, neboť body  , s nimiž se pracovalo, byly vybrány
, s nimiž se pracovalo, byly vybrány
tak, aby splňiovaly
(1)  ,
, 
a jinak zcela libovolně. Bylo tedy dokázáno, pro libovolná  splňující (1)
splňující (1)
je ![kopírovat do textarea $f(x_1) < f(x_2]$](/mathtex/e6/e653c544fa6fe2dc7fad38ee03a7852a.gif) , což podle příslušné drfinice znamená, že funkce
, což podle příslušné drfinice znamená, že funkce  je
je
v intervalu 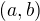 rostoucí.
rostoucí.
Offline
#3 13. 03. 2018 14:58 — Editoval BobMarley (13. 03. 2018 15:04)
Re: Lagrangeova věta - průběh funkce
↑ Rumburak:
Děkuji, myslím že rozumím -> "....byly vybrány libovolně" = pro každé  , kde
, kde  platí...
platí...
"na pozadí důkazu tedy nevolím jednu dvojici pevně x_1, x_2, ale vlastně všechny body z intervalu (a,b)"
Offline
#4 13. 03. 2018 17:01
Re: Lagrangeova věta - průběh funkce
↑ BobMarley:
Přesně tak. O číslech  jsme předpokládali pouze to, že splňují
jsme předpokládali pouze to, že splňují
(1)  ,
,  ,
,
a důkaz vyšel, aniž by bylo nutno předpokládat více. Můžeme tedy usoudit,
že tomu tak bude pro libovolnou dvojici  splňující (1).
splňující (1).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lagrangeova věta - průběh funkce (TOTO TÉMA JE VYŘEŠENÉ)