Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Lineární rovnice s absolutní hodnotou (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 03. 2018 16:16 — Editoval Vecerrov (07. 03. 2018 17:50)
- Vecerrov

- Příspěvky: 26
Lineární rovnice s absolutní hodnotou
Dobrý den,
nevím si rady s následujícím příkladem: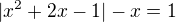
Jde mi o postup, výsledek má být {0;1}.
Předem děkuji!
Offline
- (téma jako vyřešené označil(a) zdenek1)
#3 07. 03. 2018 16:42
- Vecerrov

- Příspěvky: 26
Re: Lineární rovnice s absolutní hodnotou
A jak zjistím, jestli je řešení platné?
Offline
#4 07. 03. 2018 16:52 — Editoval laszky (07. 03. 2018 17:05)
Re: Lineární rovnice s absolutní hodnotou
Postup je dvoji mozny (omlouvam se za vyreseni celeho prikladu)
1) Absolutni hodnotu muzes odstranit dvema zpusoby - budto se zmeni znamenko, nebo nezmeni.
a) V pripade, ze se nezmeni (vnitrek je kladny), bude mit rovnice tvar 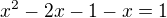 , coz je kvadraticka rovnice s koreny
, coz je kvadraticka rovnice s koreny 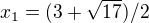 a
a 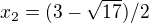 a protoze pro obe tyto hodnoty je
a protoze pro obe tyto hodnoty je  , jsou to reseni.
, jsou to reseni.
b) V pripade, ze se znamenko zmeni (vnitrek abs. hodnoty je zaporny), bude mit rovnice tvar  , coz je kvadraticka rovnice s koreny
, coz je kvadraticka rovnice s koreny  a
a 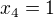 a protoze pro obe tyto hodnoty je
a protoze pro obe tyto hodnoty je  , jsou to reseni.
, jsou to reseni.
2) Druhy zpusob je nalezt koreny kvadraticke rovnice vyskytujici se v absolutni hodnote, tj.  . Ty jsou
. Ty jsou  a
a  . A uvazovat dve situace
. A uvazovat dve situace
a)  V tomto pripade je vnitrek abs. hodnoty nezaporny (cast paraboly lezici nad osou x) a odstranenim abs. hodnoty ziskame koreny
V tomto pripade je vnitrek abs. hodnoty nezaporny (cast paraboly lezici nad osou x) a odstranenim abs. hodnoty ziskame koreny  ,
,  , ktere oba lezi ve sjednoceni intervalu
, ktere oba lezi ve sjednoceni intervalu  a jsou tedy resenim.
a jsou tedy resenim.
b)  V tomto pripade je vnitrek abs. hodnoty zaporny (cast paraboly lezici pod osou x) a odstranenim abs. hodnoty ziskame koreny
V tomto pripade je vnitrek abs. hodnoty zaporny (cast paraboly lezici pod osou x) a odstranenim abs. hodnoty ziskame koreny 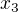 ,
, 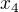 , ktere oba lezi v intervalu
, ktere oba lezi v intervalu 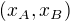 a jsou tedy resenim.
a jsou tedy resenim.
Offline
#5 07. 03. 2018 17:42
- Vecerrov

- Příspěvky: 26
Re: Lineární rovnice s absolutní hodnotou
Pomoc! Akorát se do toho víc a víc zamotávám!
Nulové body jsem určila 
Intervaly 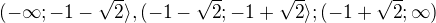
Pro interval 1 bude kladný, interval 2 záporný, interval 3 kladný
Když udělám člen v absolutní hodnotě kladný, dostanu  , -2 je v intervalu, 1 ne, tím pádem je řešením I1 a I3 číslo -2
, -2 je v intervalu, 1 ne, tím pádem je řešením I1 a I3 číslo -2
Když ho udělám naopak kladný, vyjde mi 0; -3, přičemž do I2 patří jen 0.
Tím pádem by řešení mělo být {-2;0}, ale v učebnici je {0;1}
V čem dělám chybu? Asi Vám to přijde banální, ale už mám opravdu hlavu jako balón. :(
Offline
#6 07. 03. 2018 17:47
#7 07. 03. 2018 17:50
Re: Lineární rovnice s absolutní hodnotou
↑ laszky:
Zdravím,
už jsem to ve tvých příspěvcích viděl několikrát. Dokážeš jednoduchý problém neuvěřitelně zkomplikovat.
Je až fascinující, jak dvě vysoké školy odnaučí člověka používat "selský rozum".
↑ Vecerrov:
Když si rovnici upravíš na  , vidíš, že levá strana rovnice je nezáporná, tudíž i pravá stana je nezáporná. Takže musí platit
, vidíš, že levá strana rovnice je nezáporná, tudíž i pravá stana je nezáporná. Takže musí platit  . Za této podmínky můžeš celou rovnici umocnit "na druhou" a převést na tvar
. Za této podmínky můžeš celou rovnici umocnit "na druhou" a převést na tvar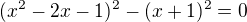
a když nyní použiješ známý vztah 
dostaneš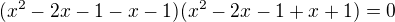
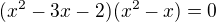
stačí vyřešit tuto rovnici a podívat se, které kořeny splňují podmínku. Máš to vyřešené na pár řádcích a nějaké rozdělování na dvě varianty vůbec nepotřebuješ.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 07. 03. 2018 17:52
- Vecerrov

- Příspěvky: 26
Re: Lineární rovnice s absolutní hodnotou
↑ zdenek1: Hrozně moc Vám děkuji! Vůbec mi nedošlo, že to tak jde!
Offline
#9 07. 03. 2018 17:59
Re: Lineární rovnice s absolutní hodnotou
↑ zdenek1:
Tvoje reseni je sice elegantni, ale obavam se, ze jakmile bude podobna rovnice s absolutni hodnotou slozitejsi (napr. vice absolutnich hodnot), nepujde pouzit a Vecerrov bude nahrana. Postup rozdelit si problem na jednotlive intervaly je univerzalni a funguje vzdy.
Offline
#11 10. 03. 2018 10:42 — Editoval jelena (10. 03. 2018 12:09)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární rovnice s absolutní hodnotou
Zdravím,
↑ zdenek1: máte s kolegou naprosto stejný způsob - oba jste vytvořili 2 rovnice k řešení (u Tebe jsou schovány v součinovém tvaru). A oba místo nalezení intervalů, na kterých řešíte, používáte kontrolu výsledku (kolega dosazením do vnitřku absolutní hodnoty, Ty - dosazením do rovnice (edit - kontrolou podmínky).
kolega laszky napsal(a):
1) Absolutni hodnotu muzes odstranit dvema zpusoby - budto se zmeni znamenko, nebo nezmeni.
a) V pripade, ze se nezmeni (vnitrek je kladny), bude mit rovnice tvar, coz je kvadraticka rovnice s koreny
a
a protoze pro obe tyto hodnoty je
, jsou to reseni.
b) V pripade, ze se znamenko zmeni (vnitrek abs. hodnoty je zaporny), bude mit rovnice tvar, coz je kvadraticka rovnice s koreny
a
a protoze pro obe tyto hodnoty je
, jsou to reseni.
Zajímavé je, že při řešení iracionálních rovnic se tato technika běžně využívá (při neekvivalentních úpravách se jen napíše podmínka a výsledek se ověřuje zkouškou), ale při absolutních hodnotách se toto neukazuje. ↑ Vecerrov: - je tak? A proto jsi se ztrácela v intervalech. Co tedy s reputaci kolegy lazsky? Děkuji.
Ještě to vypadá, že se diskutuje jiná rovnice, než je v zadání.
Vecerrov napsal(a):
Dobrý den,
nevím si rady s následujícím příkladem:
Jde mi o postup, výsledek má být {0;1}.
Předem děkuji!
Děkuji za upřesnění.
Offline
#13 17. 04. 2018 00:01 — Editoval vanok (17. 04. 2018 00:02)
Re: Lineární rovnice s absolutní hodnotou
Pozdravujem ↑ jelena:,
Zaujimava analyza situacie.
Pochopitelne methoda kolegu je zaujimava ↑ laszky: a vseobecnejsie pouzitelna ako elegantna methoda kolegu ↑ zdenek1:.
No ale treba vyzadovat od ziakov len elegantne methody?
A povedat, ze dlhsie riesenie je komplikovane v tomto pripade sa mi zda neprimerana poznamka.
Tiez navrhujem zrusit negativnu reputaciu za poctivu pomoc ktoru tu dal kolega laszky.
Tiez navrhujem vymazat posmesnu poznamku od kolegu ↑ misaH:, ktory nic nepochopil.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 17. 04. 2018 01:05
Re: Lineární rovnice s absolutní hodnotou
... malý dodatek ... všichni včetně mě (já to právě opravila) jsme měli uvedený jiný příklad než tazatel(ka). První znaménko má být plus, nikoli mínus. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#15 17. 04. 2018 01:14
Re: Lineární rovnice s absolutní hodnotou
↑ gadgetka:
Ahoj, nemyslim ze bychom to vsichni prehlidli. Vzhledem k tomu, kdy ↑ Vecerrov: naposledy editovala svuj prispevek, je pravdepodobne, ze znamenko opravila.
Offline
#16 17. 04. 2018 01:38
Re: Lineární rovnice s absolutní hodnotou
↑ laszky:
... také mě to napadlo, ale až poté, co jsem příspěvek odeslala, to jsem si všimla té editace... :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#17 25. 04. 2018 09:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární rovnice s absolutní hodnotou
Zdravím,
↑ vanok: děkuji za "+".
No ale treba vyzadovat od ziakov len elegantne methody?
Je třeba minimálně takové metody ukazovat, nebo podněcovat vlastní nápady žáků v tomto smyslu. A od kvalitních žáků a studentů samozřejmě také vyžadovat (je to kultura). Přirovnala bych to k výrobě židlí: požadujeme, aby byla stabilní a spolehlivá, bez vyčnívajících hřebíků (tedy, že řešení je správné a kompletní). Aby výroba nervala dlouho a na mistra a na jeho pracovní místo byla radost pohledět (řešení je úsporné). Potom zde máme TON (řešení je elegantní a zároveň použitelné) a ještě máme Pantona a Rietvelda (o-och a a-ach, ale sedět by na tom nechtěl nikdo - jak by vypadalo řešení uvedené rovnice v tomto přirovnání? :-)).
Kolega Zdeněk určitě nalézá elegantní způsob kontroly (podmínka  je pro kontrolu nejrychlejší). Ovšem v další úpravě již provádí operaci navíc oproti přímému použití definice absolutní hodnoty. Toto využívá kolega ↑ laszky: v metodě a). Opakuji, že pro mne bylo podstatné, že oba ukázali "nepoužití podrobného rozpisu intervalů po nalezení nulových bodů absolutní hodnoty".
je pro kontrolu nejrychlejší). Ovšem v další úpravě již provádí operaci navíc oproti přímému použití definice absolutní hodnoty. Toto využívá kolega ↑ laszky: v metodě a). Opakuji, že pro mne bylo podstatné, že oba ukázali "nepoužití podrobného rozpisu intervalů po nalezení nulových bodů absolutní hodnoty".
Tiez navrhujem zrusit negativnu reputaciu za poctivu pomoc ktoru tu dal kolega laszky.
:-) kolegů laszky zatím řadím ke kolegům schopným spočítat svíčky na narozeninovém dortu. Pokud nedovede, ať se přihlásí.
Dotaz o reputaci byl přímo na autorku tématu, nejspíš již se odhlásila z mailů k tématu.
Pěkně zdravím a omluva za prodlevu s reakci.
Offline
#19 25. 04. 2018 14:26
Re: Lineární rovnice s absolutní hodnotou
Cau ↑ laszky:,
Ale ked ti ju niekto da za poctivu pomoc, tak to nie je ferove.
Personne n'est prophète en son pays. 😂
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Lineární rovnice s absolutní hodnotou (TOTO TÉMA JE VYŘEŠENÉ)
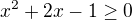 a pro případ, že
a pro případ, že  .
.