Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 05. 2018 17:38
Kombinatorika 7
Guten tag.
Mal som tu nasledujuci priklad, zdanlivo jednoduchy, overme ze uvazujem spravne:
Statna poznavacia znacka nejakeho statu sa sklada zo 3 pismen (28 moznych) a 4 cislic (10 moznych), cislice a pismena sa mozu opakovat. Kolko roznych SPZ-tiek takto vytvorime?
Riesenie bolo Variance s opakovanim (trieda, pocet prvkov) ako V'(3,28)*V'(4,10) ale ja si nemyslim ze to je spravne:
Za prve, nebereme v uvahu poziciu pismen a cislic. Ak by boli nasjkor pismena a potom cislice, napr. QWER123, tak OK. Ale Moze byt aj Q1W2E34
Takze zakladne riesenie by malo byt:
V'(3,28)*V'(4,10) * P(7) (permutacie bez poakovania zo 7 prvkov). (toto je IMO podobne ako Problem Okruhleho Stolu, ak poznate...)
Stale to nie je kompletne riesenie pretoze AAB1234 je to iste ako AAB1234 (prehodil som A-cka). Musim z riesenia vyextrahovat pripady, kjed sa mi znasobi nejaky symbol....
A ako na to... toto bude asi zaplatene...
...nie som si isty ci premyslam spravne...
Plz halp!
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
- (téma jako vyřešené označil(a) Peter_CSR)
#3 02. 05. 2018 19:10 — Editoval Peter_CSR (02. 05. 2018 20:43)
Re: Kombinatorika 7
sqrt(211) napsal(a):
O tom vyextrahování opakování ještě popřemýšlím, ale ten problém s pozicí je jednoduchý: není přece zapotřebí rozlišovat mezi číslicemi a písmeny, takže je to V'(7,28+10).
vdaka, squirt, ale nemas uplnu pravdu. V zadani je, ze mas prave 3 pismena a 4 cisla.
Myslim ze problem som vyriesil, ale poprosim o kontrolu:
- Moje pozicne riesenie je sravne.
- Druha cast je nezmysel. Variacie s opakovanim beru prave jeden pripad opakovaneho znaku na dvoch a viac miestach, napr. AAB1234, nie viac. Pekne som to doplietol. Toto sa presne stane ked hodite po cloveku vzorec bez naleziteho odvodenia
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#4 02. 05. 2018 19:26
Re: Kombinatorika 7
↑ Peter_CSR: Staci jednoducha uvaha a netreba ziadne variacie s takym alebo onakym opakovanim. Ak na prve miesto v usporiadanej dvojici mozeme dat  objektov a na druhe
objektov a na druhe  , tak mozeme vytvorit
, tak mozeme vytvorit 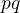 dvojic. Jasne, nie?
dvojic. Jasne, nie?
Takze v nasom pripade sa da vytvorit 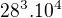 znaciek. Pripadne, ak by (ako je to pri znackach obvykle) nebolo mozne pouzit cislo
znaciek. Pripadne, ak by (ako je to pri znackach obvykle) nebolo mozne pouzit cislo  , tak o nieco menej.
, tak o nieco menej.
Offline
#5 02. 05. 2018 20:19
Re: Kombinatorika 7
↑ Peter_CSR:
Tak já to shrnu.
Řešení, které uvádíš jako oficiální (V'(3,28)*V'(4,10) ) a které uvádí ↑ vlado_bb: (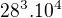 ) (obojí je stejné)
) (obojí je stejné)
by se týkalo zadání, kde je nejprve trojice písmen následovaná čtveřicí číslic (případně naopak, nebo jakkoli, kde jsou jasně předem určené pozice pro čísla a písmena). Což v textu úlohy není.
Pokud pozice nejsou předem dané (tak jak o tom uvažuješ v prvním příspěvku), musíš ty pozice nejprve vybrat.
vybereme pozice pro písmena 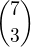 možností
možností
umístíme písmena 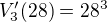 možností
možností
umístíme číslice 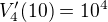 možností
možností
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 02. 05. 2018 20:48
Re: Kombinatorika 7
↑ zdenek1:
vecsine rozumiem ale som dnes trocha unaveny takze hlupa otazka... : preco vyberame pozicie kombinaciami? ja to tam v tejto chvili nejak nevidim...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#7 02. 05. 2018 20:55
Re: Kombinatorika 7
vlado_bb napsal(a):
↑ Peter_CSR: Staci jednoducha uvaha a netreba ziadne variacie s takym alebo onakym opakovanim. Ak na prve miesto v usporiadanej dvojici mozeme dat
objektov a na druhe
, tak mozeme vytvorit
dvojic. Jasne, nie?
Takze v nasom pripade sa da vytvoritznaciek. Pripadne, ak by (ako je to pri znackach obvykle) nebolo mozne pouzit cislo
, tak o nieco menej.
ok.
Ako by sa ale riesenie zmenilo, keby sme stanovili, ze jednotlive symboly sa mozu v retazci vyskytnut najviac dva krat?
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#8 02. 05. 2018 21:06 — Editoval Peter_CSR (02. 05. 2018 21:14)
Re: Kombinatorika 7
↑ Peter_CSR:
ospravedlnujem sa ze sa tak tupo pytam ale toto su problemy typu bud alebo.
Jedno riesenie co ma napada je 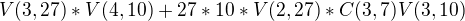
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#9 02. 05. 2018 21:14
Offline
#10 02. 05. 2018 21:39
Re: Kombinatorika 7
↑ Peter_CSR: Zislo by sa upresnit zadanie. Su teda aj znacky 34A49AB pripustne?
Offline
#11 03. 05. 2018 08:56 — Editoval Peter_CSR (03. 05. 2018 09:12)
Re: Kombinatorika 7
vlado_bb napsal(a):
↑ Peter_CSR: Zislo by sa upresnit zadanie. Su teda aj znacky 34A49AB pripustne?
rozumiem.
Zadanie je:
- mas 7-miestny kod.
- Pouzivas presne 3 pismena z 27 a 4 cislice z 10 na akejkolvek pozicii v kode.
- davam rozsirujucu podmienku (len tak zo zvedavosti) a to ze kazdy znak sa vyskytuje maximalne 2 krat.
myslim ze toto je skor uloha na analiticky pristup nez stredoskolsku algebru ale myslim zepre rozne ucely by mohlo byt zaujmave vediet postup.
a) najskor vypocitam pripad pre vyskyt symbolov prave raz: C(3,7)*V(3,27)*V(4,10) (Kombinacie bez opakovania 3. triedy z 7 prvkov, obdobne Variacie bez opakovania)
b) Pripocitam pripad ked sa nahodny symbol vyskytne 2 razy. Musim roizlisovat pripad kedy sa zdvoji cislica a kedy pismeno.
b1) zdvoji sa pismeno:
- Vypocitam na ktorych poziciach moze zdvojenie nastat C(2,7)
- Moze sa mi zdvojit 27 pismen
- ostava mi 5 miest na ktore umiestnujem unikatne pismena C(2,5)
- vynasobim s variaciami utvorenymi zo zvysnych 26 pismen na 2 poziciach ktore mi kod dovoluje: V(2,26)
- Vynasobim s variaciami cislic V(4,10)
b2) obdobnym sposobom by som postupoval pre pripad kde sa zdvojuju cislice.
Vysledny pocet moznych kodov bude P = pocet kodov utvorenych z unikatnych symbolov(a) + pocet kodov utvorenych zo zvojenych pismen(b1) + pocet kodov utvorenych zo zdvojenych cislic(b2)
Keby sa mi pismena opakovali 1,2,3 krat a cislice 1,2,3,4 krat musel by som obdobnou metodou pocitat pripady pre 1,2,3 nasobne opakovanie pismien a 1,2,3,4 opakovanie cislic.
OK, malo by to davit zmysel, aj ked som si nie isty ci matematikovi. Ospravedlnujem sa, toto je najskaredsia vec ktoru som na toto forum kedy napisal a to som uz uvazoval ci moze mocninova funkcia mat zaporny zaklad. A tiez dovod preco programatori nerobia matiku....
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#12 03. 05. 2018 09:00
Re: Kombinatorika 7
↑ Peter_CSR: Mame teda 38 znakov a 7 pozicii. Na kazdej pozicii ma byt jeden znak. To je spolu 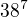 moznosti. Preco to tak priserne komplikujes?
moznosti. Preco to tak priserne komplikujes?
Offline
#13 03. 05. 2018 09:14
Re: Kombinatorika 7
vlado_bb napsal(a):
↑ Peter_CSR: Mame teda 38 znakov a 7 pozicii. Na kazdej pozicii ma byt jeden znak. To je spolu
moznosti. Preco to tak priserne komplikujes?
pretoze som programator a je to nasa praca.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#14 03. 05. 2018 09:16 Příspěvek uživatele Peter_CSR byl skryt uživatelem Peter_CSR.
#15 03. 05. 2018 11:00
Re: Kombinatorika 7
↑ vlado_bb:, je to tak komplikované, protože nejde jednoduše „smíchat“ písmena a číslice (jak jsem si ze začátku taky myslel) - použijí se vždy tři písmena a čtyři číslice, takže nemůže vzniknout např. pouze číselný kód.
Ještě mě napadá jeden přístup: kombinacemi s opakováním vyberu znaky, které chci použít. U těchto kombinací lze ještě měnit pořadí, takže pro každou takovou kombinaci uděláme ještě permutace s opakováním.
Příklad:
Kombinace A,B,B,2,2,2,4 má 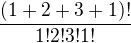 permutací... a do háje! Teď mi došlo, že bychom ty permutace museli dělat pro každou kombinaci zvlášť, protože každá kombinace bude mít jiný počet stejných prvků...
permutací... a do háje! Teď mi došlo, že bychom ty permutace museli dělat pro každou kombinaci zvlášť, protože každá kombinace bude mít jiný počet stejných prvků...
Tak jsme zase tam, kde jsme byli.
Offline
#16 03. 05. 2018 11:10
#17 03. 05. 2018 11:22
Re: Kombinatorika 7
↑ sqrt(211):
Co to tady řešíte, vždy't jsem vám to v příspěvku #5 vyřešil.
Ale pro vjistotu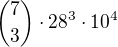
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#18 03. 05. 2018 11:39 — Editoval sqrt(211) (03. 05. 2018 11:41)
Re: Kombinatorika 7
↑ zdenek1: Pardon, v té spoustě teorií jsem to přehlédl - naivně jsem se domníval, že debata postupuje směrem k výsledku a že stačí reagovat na poslední příspěvek.
Teď jsem se na to pořádně podíval a vidím, že se to celé zvrtlo právě po příspěvku #5, který autor tématu nepochopil a my ostatní, místo abychom mu to vysvětlili, jsme začali předkládat jiné teorie, které však nebyly dotažené do konce).
Takže, vraťme se k #5, TO JE SPRÁVNÝ VÝSLEDEK. A jestli mu někdo neporozuměl dovolil bych si upřesnit:
-pozice vybíráme kombinacemi - chceme zjistit, na kterých pozicích budou písmena a na kterých čísla, tedy jestli pořadí bude p,p,p,č,č,č,č nebo třeba č,p,č,č,p,p,č atd. (p=písmeno, č=číslo).
-a pak každou takovouto kombinaci obsadíme čísly a písmeny (pomocí variací s opakováním).
Doufám, že teď už to snad bude konečně jasné a můžeme toto téma uzavřít.
Offline
#19 03. 05. 2018 12:14 — Editoval Peter_CSR (03. 05. 2018 13:05)
Re: Kombinatorika 7
Presne ako napisal Squirt.
Porozumel som Vladovmu a Zdenkovmu rieseniu. Na otazku na Zdenka a k jeho kombinaciam - uz som pochopil.
Potom som rozsiril ulohu o moju arbitrary bullshit podmienku a problem som znova vyriesil (domnievam sa, dava mi to zmysel).
Quod Erat Demonstrandum.
Dakujem vsetkym.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#20 03. 05. 2018 12:16
Re: Kombinatorika 7
sqrt(211) napsal(a):
↑ vlado_bb:, je to tak komplikované, protože nejde jednoduše „smíchat“ písmena a číslice (jak jsem si ze začátku taky myslel) - použijí se vždy tři písmena a čtyři číslice, takže nemůže vzniknout např. pouze číselný kód.
Ještě mě napadá jeden přístup: kombinacemi s opakováním vyberu znaky, které chci použít. U těchto kombinací lze ještě měnit pořadí, takže pro každou takovou kombinaci uděláme ještě permutace s opakováním.
Příklad:
Kombinace A,B,B,2,2,2,4 mápermutací... a do háje! Teď mi došlo, že bychom ty permutace museli dělat pro každou kombinaci zvlášť, protože každá kombinace bude mít jiný počet stejných prvků...
Tak jsme zase tam, kde jsme byli.
A toto je skvely napad!!! Vyrazne to zjednodusi riesenie!!
Parada a diky moc!!!
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#21 03. 05. 2018 13:06
Re: Kombinatorika 7
↑ Peter_CSR:
pockat, nemozem pouzit squirtovu metodu a to proste pre to, ze neviem ci sa mi zdvoji pismeno alebo cislo... mam dane PRAVE TRI pismena a PRAVE STYRI cisla...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
