Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 05. 2018 22:16
Goniometrická rovnice
Ahoj
mám vypočítat tenhle příklad
sin 2x=1 a mám zjistit kolik bude tg x.
Vím ,že sin 2x = 2*sin x *cos x a tg x = sin x/cos x ,ale nevím jak dosáhnout správného výsledku.
Postupoval jsem takhle:
2*sin x*cos x=1 / *(1/cos^2 x)
potom mi vyšlo:
2*tg x = 1/cos^2 x
Ale tady se zaseknu a nevím jak dál.
Jak bych měl prosím postupovat?
Offline
- (téma jako vyřešené označil(a) Erodos)
#6 24. 05. 2018 02:24 — Editoval gadgetka (24. 05. 2018 02:25)
Re: Goniometrická rovnice
↑ MichalAld:
Tyto úlohy se řeší bez prvotního vyřešení "x"... :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#8 24. 05. 2018 18:28
#9 24. 05. 2018 18:32
#10 24. 05. 2018 18:33 Příspěvek uživatele laszky byl skryt uživatelem laszky. Důvod: Predchozi text zmenen
#11 24. 05. 2018 18:35
#12 24. 05. 2018 18:43
Re: Goniometrická rovnice
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#13 24. 05. 2018 18:59
Offline
#14 24. 05. 2018 19:10 — Editoval Peter_CSR (24. 05. 2018 19:12) Příspěvek uživatele Peter_CSR byl skryt uživatelem Peter_CSR.
#15 24. 05. 2018 19:18 — Editoval Peter_CSR (24. 05. 2018 19:32)
Re: Goniometrická rovnice
↑ gadgetka:
oh, vďaka, už vidím, kde som spravil chybu :) . Zle som odmocnil..
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#16 24. 05. 2018 19:23
Re: Goniometrická rovnice
↑ Peter_CSR:
Zdravím,
je to čitelné a chybné. 
A teď musíš odmocnit, nikoli umocnit. Nezapomeň na absolutní hodnotu na levé straně rovnice.
Offline
#17 24. 05. 2018 19:36
Re: Goniometrická rovnice
↑ Al1:
ahoj, presne ako píšeš.
Tvoju rovnicu sa mi ešte stále nepodarilo upraviť...hmm...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline

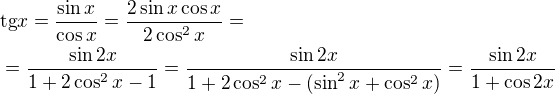


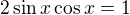
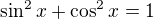
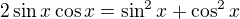
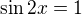
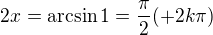



 a teda
a teda  a
a 
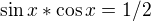 čo znamená že uhol je
čo znamená že uhol je 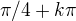 . A teda
. A teda 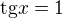
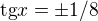 ... neviem čo robím zle, všetko mi sedí... a tvoj spôsob som nevedel upraviť...
... neviem čo robím zle, všetko mi sedí... a tvoj spôsob som nevedel upraviť... resp.
resp.  ?
?