Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2018 20:17 — Editoval Peter_CSR (25. 05. 2018 20:18)
logaritmovanie
Ahoj...toto bude jedna z tých otázok, ktoré by som si prial sa spýtať spolužiaka, pod lavicou a veľmi potichu ale...
v nasledujúcom riešení:
je toto korektný postup, alebo musím zlogaritmovať celú ľavú a celú pravú stranu, teda rovnako ako by som umocňoval?)
viem, že je to extrémne hlúpa otázka, ale nikde sa o tom nič nepíše a mňa to napadlo proste práve teraz...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
- (téma jako vyřešené označil(a) Peter_CSR)
#2 25. 05. 2018 20:44
Re: logaritmovanie
↑ Peter_CSR:
Ahoj, musíš zlogaritmovat celou levou a celou pravou stranu rovnice, jinak se nejedna o ekvivalentni úpravu rovnice
Offline
#3 25. 05. 2018 20:53 — Editoval Peter_CSR (25. 05. 2018 20:54)
Re: logaritmovanie
↑ BobMarley:
čo znamená ekvivalentná úprava? Myslel som, že je to taká úprava, ktorá nijak nemení pravdivostnú hodnotu výrazu.
napr. výraz 
možme upraviť 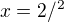
a dostaneme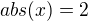
je zjavné, že pôvodná rovnica mala jediné riešenie ![kopírovat do textarea $M = [{2}]$](/mathtex/c5/c5e0c98fb566f2c47c2b4619d85317b0.gif) , zatiaľ čo po neekvivaletne úprave máme
, zatiaľ čo po neekvivaletne úprave máme ![kopírovat do textarea $M = [{-2,2}]$](/mathtex/71/7185c6a68e64d4815df75043bec6a98b.gif) a teda musíme urobiť skúšku správnosti, aby sme v pôvodnej rovnici zistili, ktorá množina je tá správna.
a teda musíme urobiť skúšku správnosti, aby sme v pôvodnej rovnici zistili, ktorá množina je tá správna.
Myslím, že rovnako to platí aj u logaritmovania, teda sa jedná o neekvivalentný typ úpravy.
S právne?
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#4 25. 05. 2018 21:05
Re: logaritmovanie
↑ Peter_CSR:
Ano, to je pravda (až na to, že ekvivalentní nebo důsledkové úpravy se aplikují na rovnici, ne na výrazy).
Aby logaritmování bylo ekvivalentní úpravou tak musí být splněno  . Jinak je to důsledková úprava.
. Jinak je to důsledková úprava.
Tyto úpravy se aplikují na celé strany rovnic:
a logaritmus rozdílu není podíl logaritmu.
Platí, že
logaritmus podílu je rozdíl logaritmů.
Offline
#5 25. 05. 2018 21:14
Re: logaritmovanie
↑ Peter_CSR:
Zdravím,
pokud chceš rovnici logaritmovat, nemůžeš napsat, že násobíš logaritmem viz tvůj první příspěvek. Navíc je hned vidět, že ti vyšel chybný výsledek, neboť 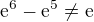 . Zkus si spočítat třeba
. Zkus si spočítat třeba . Určitě to nebude rovno 2.
. Určitě to nebude rovno 2.
Offline
#6 25. 05. 2018 21:45
Re: logaritmovanie
↑ Al1:
áno, to je od pohľadu vidieť že násobím  niečím, čo je väčšie než 1. ten zápis bol skôr symbolický...
niečím, čo je väčšie než 1. ten zápis bol skôr symbolický...
...ok teda, vidím. Hej, vidím že je to trápna otázka, ale toto je IMO jedna z týh vecí "vieš/nevieš". A ja som sa nad tým akosi zamyslel len teraz... :/
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#7 26. 05. 2018 09:44
Re: logaritmovanie
↑ Peter_CSR:
Ani na první ani na druhý pihled nevidím, že bys násobil číslem 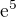 . A jaký význam má, že je to číslo větší než 1?
. A jaký význam má, že je to číslo větší než 1?
Myslím, z ostatních tvých příspěvků jsem nabyl toho dojmu, že se snažíš postavit luxusní vilu na velice nestabilních základech.
Offline
#8 26. 05. 2018 10:02
Re: logaritmovanie
↑ Peter_CSR:
Prostě představa že F(x+y) = F(x) + F(y) je úplně chybná. Neplatí to pro logaritmus, a neplatí to ani pro žádnou jinou funkci, s jedinou výjimkou - platí to jen pro násobení.
Takže neplatí ani tvé 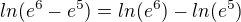
Offline
#9 26. 05. 2018 14:08
Re: logaritmovanie
Al1 napsal(a):
↑ Peter_CSR:
Ani na první ani na druhý pihled nevidím, že bys násobil číslem. A jaký význam má, že je to číslo větší než 1?
Myslím, z ostatních tvých příspěvků jsem nabyl toho dojmu, že se snažíš postavit luxusní vilu na velice nestabilních základech.
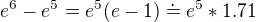
pokiaľ násobím číslo , ktoré je zjavne väčšie než
, ktoré je zjavne väčšie než  (asi 54-krát) číslom väčším než jedna, musí mi vyjsť ešte väčšie číslo a potom
(asi 54-krát) číslom väčším než jedna, musí mi vyjsť ešte väčšie číslo a potom 
skutočne nedáva význam
moje otázky sú:
a) čo je na tom, prosím, zle?
b) ak je tvoja odpoveď "nič", vysvetli mi, prosím, veľmi podrobne, čo si myslel onou citáciou.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#10 26. 05. 2018 15:08
Re: logaritmovanie
↑ Peter_CSR: Ved predsa ↑ MichalAld: napisal, co je na tom zle. Ale pokojne este raz - jedine zobrazenie v  pre ktore je
pre ktore je 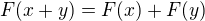 je nasobenie, teda zobrazenie
je nasobenie, teda zobrazenie 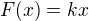 , kde
, kde  . Ziadne ine.
. Ziadne ine.
Offline
#11 26. 05. 2018 18:41 — Editoval misaH (26. 05. 2018 18:42)
- misaH
- Příspěvky: 13459
Re: logaritmovanie
↑ Peter_CSR:
Naozaj nechápeš?!
Proste neplatí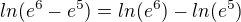
Stačí to vypočítať.
Mal si logaritmovať pravú stranu rovnice a súčasne ľavú stranu rovnice.
Teda si mal riešiť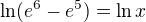
a nie to, čo si v skutočnosti riešil.
Už to tu viackrát zaznelo...
Offline
#12 26. 05. 2018 19:27
Re: logaritmovanie
↑ Peter_CSR:
Když se zamyslíš, tak zjistíš, že nebylo proč logaritmovat, hodnotu x jsi znal už nazačátku. To je, jako kdybys chtěl řešit x= 15. Co je na tom k řešení? Pokud je to rovnice, je vyřešená. Pokud je takto zapsán výraz, také není co řesit. Výraz se dá upravit jen tak, aby v každém kroku platila ekvivalence.
Jak by ti bylo, kdybys měl platit v obchodě částku x=500 (penízků) a prodavač provedl úpravu: vynásobím stem.
Podle tebe je to možná úprava.
Offline
