Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Věta o implicitní funkci - význam znění (TOTO TÉMA JE VYŘEŠENÉ)
#4 27. 05. 2018 23:15
Re: Věta o implicitní funkci - význam znění
Pak jsi v situaci napr.  a chces najit
a chces najit  ,
,  , aby
, aby  na nejakem okoli, OK? Pokud ale F zobrazuje do R (ma jen jednu slozku), pak je to trivialni, protoze napr. y_2 si zvolim konstantni a na y_1 pouziju klasickou vetu o impl. fci. Je videt, ze v tomhle pripade mam moc volnosti...spravne zobecneni je tedy uvazovat F jako zobrazeni do R2 (nebo obecne tolik, kolik mam "implicitnich promennych"). Pak ale predpoklad nenulovosti derivace se preklada jako nenulovost determinantu z
na nejakem okoli, OK? Pokud ale F zobrazuje do R (ma jen jednu slozku), pak je to trivialni, protoze napr. y_2 si zvolim konstantni a na y_1 pouziju klasickou vetu o impl. fci. Je videt, ze v tomhle pripade mam moc volnosti...spravne zobecneni je tedy uvazovat F jako zobrazeni do R2 (nebo obecne tolik, kolik mam "implicitnich promennych"). Pak ale predpoklad nenulovosti derivace se preklada jako nenulovost determinantu z 
Offline
#5 27. 05. 2018 23:22
Re: Věta o implicitní funkci - význam znění
Jojo, tu větu máme vlastně také, ještě bych měl dotaz k důkazu, na konci, kde se dostáváme k rovnosti  , kde tedy rovnost nule platí pro všechny x z okolí
, kde tedy rovnost nule platí pro všechny x z okolí  a
a  , tak ona rovnost nule platí, protože v předpokladu je ona rovnost pro
, tak ona rovnost nule platí, protože v předpokladu je ona rovnost pro  a
a  a díky spojitosti a monotonii na okolí to platí i pro všechny
a díky spojitosti a monotonii na okolí to platí i pro všechny  z okolí?
z okolí?
Offline
#7 27. 05. 2018 23:31
Re: Věta o implicitní funkci - význam znění
Pardon, to jsem se vyjádřil nepřesně, tu mezičást, která to řeší jsem vynechal, bereme to dejme tomu pro derivaci kladnou, tedy funkce je rostoucí, z toho odvodíme, že je rostoucí pro okolí bodu x, y, poté zúžíme okolí, je rostoucí pro všechny body v okolí a pak nastává ona rovnost u níž si nejsem jist z čeho plyne.↑ Bati:
Offline
#8 27. 05. 2018 23:40
Re: Věta o implicitní funkci - význam znění
↑ m.sey:
Ta rovnost se musi nejak "zkonstruovat" vhodnou volbou  . Myslim, ze se to dela pres vetu o stredni hodnote..kdyz tedy z predpokladu vim, ze pro nejake pevne
. Myslim, ze se to dela pres vetu o stredni hodnote..kdyz tedy z predpokladu vim, ze pro nejake pevne  je
je  a
a  , tak bude existovat
, tak bude existovat  mezi tak, ze
mezi tak, ze  . A ted to same udelam pro vsechny x, cimz definuju
. A ted to same udelam pro vsechny x, cimz definuju 
Offline
#9 27. 05. 2018 23:47
Re: Věta o implicitní funkci - význam znění
V některých verzích vlastně je a teď si jenom nejsem jist jestli je potřeba, jestli prostě nestačí spojitost a monotonie abychom mohli tvrdit, že platí ona rovnost nule pro všechny body z okolí.↑ Bati:
Offline
#12 28. 05. 2018 00:11
Re: Věta o implicitní funkci - význam znění
↑ m.sey:
No to je ono...pro kazde x z nejakeho okoli se zkonstruuje 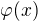 pomoci vety, ze kdyz je spojita funkce a
pomoci vety, ze kdyz je spojita funkce a  , pak existuje
, pak existuje ![kopírovat do textarea $c\in[a,b]$](/mathtex/94/94f07e0bf15bc9ff32c4ab41ca28fa44.gif) , ze
, ze  ...to jsem myslel tou vetou o stedni hodnote...ale asi se to jmenuje veta o nabyvani mezihodnot, nebo to ma i nejake jmenu
...to jsem myslel tou vetou o stedni hodnote...ale asi se to jmenuje veta o nabyvani mezihodnot, nebo to ma i nejake jmenu
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Věta o implicitní funkci - význam znění (TOTO TÉMA JE VYŘEŠENÉ)

 a
a  ?
? , napr.
, napr. a u
a u  jedná se o rovnost nule na posledním (vlnovkou) podtrženém řádku a nejsem si jist z čeho plyne.
jedná se o rovnost nule na posledním (vlnovkou) podtrženém řádku a nejsem si jist z čeho plyne.