Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Střed kružnice opsané - způsob výpočtu (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 10. 2018 21:07
Střed kružnice opsané - způsob výpočtu
Ahoj. Mám příklad:
Urči střed kružnice opsané trojúhelníku ABC, A [3;1], B [2;–2], C [6;6]. Vím, že stačí vytvořit soustavu 3 obecných rovnic kružnice k vyřešení. Ale napadl mě další způsob, který mi ale nevychází. Chtěl bych se tedy zeptat, zda je způsob špatný, nebo dělám pouze chybu ve výpočtu.
Napadlo mě spočítat střed bodu AB. Z AB udělat vektor, z něho pak normálový a udělat obecnou rovnici přímky, do které dosadím právě střed AB. Potom bych udělal totéž s CB - střed CB a normálový vektor + obecná rovnice se středem CB.
Potom soustavu těchto dvou rovnic. Po výpočtu vyjdou body, které by měly být středem kružnice.
Co myslíte, je způsob správný?
Správný střed je [22;-7]
Díky.
Offline
- (téma jako vyřešené označil(a) Dobson)
#2 06. 10. 2018 21:32
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Střed kružnice opsané - způsob výpočtu
Áno, aj toto je spôsob ako nájsť stred kružnice opísanej trojuholníku.
BTW riešením sústavy dvoch rôznobežných priamok je vždy len jeden bod.
Offline
#3 06. 10. 2018 22:36 — Editoval misaH (06. 10. 2018 22:36)
- misaH
- Příspěvky: 13459
Re: Střed kružnice opsané - způsob výpočtu
↑ Ferdish:
No a ešte 1 BTW ... stred bodu AB neexistuje :-)
Ten "ich" stred je správny...
Offline
#4 06. 10. 2018 22:40
Re: Střed kružnice opsané - způsob výpočtu
↑ Dobson:
Dobrý večer. Váš postup je v podstatě výpočtem průsečíku os dvou stran trojúhelníku, které se protínají ve středu kružnice trojúhelníku opsané. Pro zajímavost uvádím další podobný postup.
Lze vyjít i z toho, že osa úsečky je množinou bodů stejně vzdálených od krajních bodů úsečky a z toho odvodit její rovnici (pro zjednodušení je možno při výpočtu uvažovat i čtverec vzdálenosti - výsledek bude tentýž):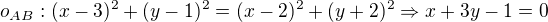
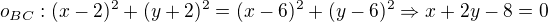
![kopírovat do textarea $\Rightarrow S[22;-7]$](/mathtex/16/16843a149958ce4ddd9c412e4704d636.gif)
V podstatě se zapsané výrazy jen zjednoduší umocněním, kvadratické členy na obou stranách se vyruší a po drobné úpravě hned máme obecné rovnice dvou os stran trojúhelníku a můžeme spočítat jejich průsečík.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Střed kružnice opsané - způsob výpočtu (TOTO TÉMA JE VYŘEŠENÉ)