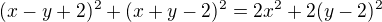Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 10. 2018 14:53
kuželosečky
Achjo, prosím o radu s kuželosečkama. Z obyčejně zadané rovnice to dokážu vypočítat, ale tohle je nějaká pro mou osobu nepochopitelná.
ZADÁNÍ: Napište rovnici kružnice ve středovém tvaru a určete souřadnice středu S a velikost poloměru r.
1) 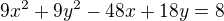 VÝSLEDEK: S(
VÝSLEDEK: S( ,-1), r=3
,-1), r=3
2)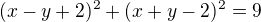 VÝSLEDEK: S(0,2), r=
VÝSLEDEK: S(0,2), r=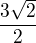
Pomohla by mi chytrá hlavička :) děkuji
Offline
- (téma jako vyřešené označil(a) ebabuli)
#2 20. 10. 2018 15:29 — Editoval misaH (20. 10. 2018 18:02)
- misaH
- Příspěvky: 13459
Re: kuželosečky
↑ ebabuli:
No.
Do 1 témy len 1 úloha, aby sa komenty neplietli.
1)
Doplň do úplného štvorca pre x aj y...
Nápoveda pre x: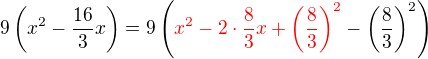
Offline
#3 20. 10. 2018 15:30 — Editoval laszky (20. 10. 2018 16:10)
#5 20. 10. 2018 16:13 — Editoval misaH (20. 10. 2018 16:16)
- misaH
- Příspěvky: 13459
Re: kuželosečky
↑ ebabuli:
Ten môj postup ti nič nehovorí?
Potrebuješ rovnicu v tvare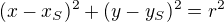
U príkladu 1 ju dostaneš klasickým doplnením do štvorca.
Pre y je to ľahké, pre x som ti začiatok naznačila.
Naľavo necháš len druhé mocniny, všetky čísla dáš doprava - ich hodnota je druhá mocnina polomeru.
Offline
#8 20. 10. 2018 16:21
Re: kuželosečky
↑ misaH: no píšou to tady a jde to tak :) https://www.e-matematika.cz/stredni-sko … edovou.php
Offline
#9 20. 10. 2018 16:22
- misaH
- Příspěvky: 13459
Re: kuželosečky
↑ ebabuli:
No.
Po úprave som dostala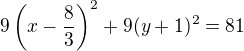
Stačí vydeliť deviatimi a rovnica je na svete.
Offline
#10 20. 10. 2018 16:23
- misaH
- Příspěvky: 13459
Re: kuželosečky
↑ ebabuli:
Aha - tak to je súčasť úpravy na úplný štvorec...
Offline
#12 20. 10. 2018 16:27 — Editoval misaH (20. 10. 2018 16:34)
- misaH
- Příspěvky: 13459
Re: kuželosečky
My sme sa to učili tak, že napríklad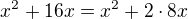
a toto je začiatok rozpisu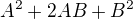
Takto sa vlastne príde na to B, v mojej ukážke B=8, lebo A je evidentne rovné x.
Pokračovanie: Úplný štvorec je 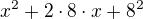
Ale pretože sme 8 na druhú pridali, musíme ho od úplného štvorca odobrať: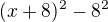
Offline
#14 20. 10. 2018 16:33
- misaH
- Příspěvky: 13459
Re: kuželosečky
↑ ebabuli:
Tvoj príklad je zložitejší - buď na začiatku hneď vydelíš deviatkou aby si mala pri x na druhú aj y na druhú neviditeľné číslo 1 alebo deviatku len vyjmeš a úpravu na štvorec robíš vnútri zátvorky.
Polomer dostaneš tak, že všetky čísla zľava prenesieš doprava, to bude druhä mocnina polomeru.
Veď to píšem vyššie...
Offline
#16 20. 10. 2018 16:38 — Editoval misaH (20. 10. 2018 16:45)
- misaH
- Příspěvky: 13459
Re: kuželosečky
↑ ebabuli:
:-)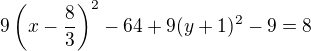
Ja som postupovala vyňatím 9 a úpravy som robila vnútri v zátvorke: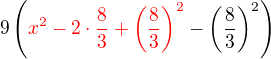
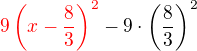
Offline