Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 10. 2018 23:37 — Editoval laszky (23. 10. 2018 23:42)
Re: kuželosečky5
↑ ebabuli:
Ahoj, pokud se dotyka osy x v bode [1,0], potom musi mit stred kruznice x-ovou souradnici rovnou jedne a polomer kruznice bude roven (absolutni hodnote) y-ove souradnice stredu.
Offline
#4 24. 10. 2018 01:24 — Editoval Ferdish (24. 10. 2018 01:35)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: kuželosečky5
↑ ebabuli:
V tomto druhom prípade by (analogicky) y-ová súradnica stredu bola rovná 3, a polomer rovný absolútnej hodnote x-ovej súradnici stredu.
Základom takýchto úloh je vždy obrázok/náčrt, z ktorého by to malo byť už zrejmé. Skús si teda obe zmienené kružnice zakresliť do súradnicovej sústavy...
Offline
#5 24. 10. 2018 11:39 — Editoval Rumburak (25. 10. 2018 14:32)
Re: kuželosečky5
↑ ebabuli:
Ahoj. Šel bych na to přísně analyticky (aby ses naučila tuto metodu pro složitější úlohy).
Každá kružnice v rovině opatřené kartéskou soustavou souřadnic má nějaký střed ![kopírovat do textarea $S[m,n]$](/mathtex/35/351eac6911e7a00a1dee8ef3b4662c54.gif)
a nějaký poloměr  , při čemž její rovnici je možno vyjádřit ve tvaru
, při čemž její rovnici je možno vyjádřit ve tvaru
(A)  .
.
Podmínka "prochází bodem ![kopírovat do textarea $[2,1]$](/mathtex/d6/d6cee0a0facc107669a832ebaba8ece8.gif) " dle (A) znamená, že musí být splněna rovnice
" dle (A) znamená, že musí být splněna rovnice
(1)  .
.
Z podmínky "dotýká se osy  v bodě
v bodě ![kopírovat do textarea $[1,0]$](/mathtex/91/91a3ccdf14346c86322c0b6d2675b569.gif) " plynou dvě věci:
" plynou dvě věci:
jadnak že hledaná kružnice uvedeným bodem prochází, což vede k rovnici
(2)  ,
,
a dále že bod ![kopírovat do textarea $[1,0]$](/mathtex/91/91a3ccdf14346c86322c0b6d2675b569.gif) je jediným společným bodem kružnice (A) a osy
je jediným společným bodem kružnice (A) a osy  , jinými slovy:
, jinými slovy:
je-li ![kopírovat do textarea $[x, 0]$](/mathtex/c9/c99744ecf32180cdc02eba857432a2ae.gif) bodem hledané kružnice, potom
bodem hledané kružnice, potom 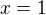 . To znamená. že rovnice
. To znamená. že rovnice
(B) 
(ekvivalentně upravitelná na kvadratickou rovnice s naznámou  a parametry
a parametry  )
)
má jediné řešení (a sice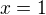 ). To vede k podmínce na diskriminant
). To vede k podmínce na diskriminant 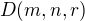 této
této
kvadratické rovnice, a sice k podmínce
(3) 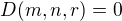 .
.
Rovnice (1), (2, (3) tvoří soustavu tří rovnic o třech neznámých, kterou vyřešíme.
Offline
#6 24. 10. 2018 20:08
Re: kuželosečky5
↑ Rumburak: no tak se na mne musí hezky polopatě ;) takže budu mít 3 rovnice 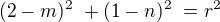 pod ní hned druhou
pod ní hned druhou 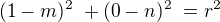 a třetí jsem teda nepobrala :(
a třetí jsem teda nepobrala :(
Offline
#7 24. 10. 2018 22:11 — Editoval Al1 (25. 10. 2018 13:36)
Re: kuželosečky5
↑ ebabuli:
Zdravím,
máš celou situaci nakreslenou, jak ti radil kolega ↑ Ferdish:?
Zde je podobná situace (volil jsem záměrně jinou kružnici, i když bod dotyku jsem nechal stejný)
Z něho je patrné, že pokud je střed kružnice ![kopírovat do textarea $S[m,n]$](/mathtex/35/351eac6911e7a00a1dee8ef3b4662c54.gif) a kružnice se dotýká osy x v bodě
a kružnice se dotýká osy x v bodě ![kopírovat do textarea $[1,0]$](/mathtex/91/91a3ccdf14346c86322c0b6d2675b569.gif) , pak platí, že m=1. A když se podíváš na poloměr kružnice (zde r=3) a druhou souřadnici středu zjistíš, že musí platit: r=n.
, pak platí, že m=1. A když se podíváš na poloměr kružnice (zde r=3) a druhou souřadnici středu zjistíš, že musí platit: r=n.
Proto daná rovnice má tvar 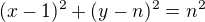 (opět viz kolega ↑ Ferdish:). Nyní stačí do této rovnice dosadit bod
(opět viz kolega ↑ Ferdish:). Nyní stačí do této rovnice dosadit bod ![kopírovat do textarea $[2,1]$](/mathtex/d6/d6cee0a0facc107669a832ebaba8ece8.gif) . Máš jednu rovnici pro jednu neznámou.
. Máš jednu rovnici pro jednu neznámou.
Offline
#8 25. 10. 2018 10:58 — Editoval Rumburak (25. 10. 2018 11:38)
Re: kuželosečky5
↑ ebabuli:
Rovnici 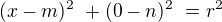 nejprve upravíme na tvar
nejprve upravíme na tvar
 .
.
Diskriminantem této kvadratické rovnice bude (podle příslušného vzorce, který bys měla znát)
 .
.
Platí věta: Kvadratická rovnice má jediné řešení právě tehdy, je-li její diskriminant roven 0.
Odtud ona třetí rovnice
 .
.
Offline
#9 25. 10. 2018 13:48 — Editoval gadgetka (25. 10. 2018 13:53)
Re: kuželosečky5
Zdravím, příklad můžeš řešit i přes vzdálenost dvou bodů, ze zadání musí platit, že 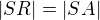 , kde bod A je bod dotyku s osou x.
, kde bod A je bod dotyku s osou x.![kopírovat do textarea $S[x; y]$](/mathtex/46/4638aea6024992caa1d04764ce2204fd.gif)
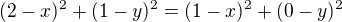
Do rovnice přímky, která je řešením rovnice, pak stačí dosadit x-ovou souřadnici středu, která je jasná ze zadání a dopočítat souřadnici y-ovou. :)
P. S. Případně už můžeš vyjít ze souřadnic středu S[1; 0] a ulehčit si výpočet. :)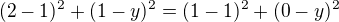
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
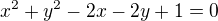 zkoušela jsem soustavu rovnic ale někde bude zase zádrhel
zkoušela jsem soustavu rovnic ale někde bude zase zádrhel