Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Infimum a supremum R, N a prázdné množiny (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 10. 2018 11:33
Infimum a supremum R, N a prázdné množiny
Zdravím,
mám za úkol určit infimum a supremum u množiny přirozených (N) a reálných (R) čísel a u prázdné množiny. Dočetl jsem se, že u přirozených čísel je infimem -nekonečno a supremem +nekonečno a u prázdné množiny je to prý naopak. Jenže nevím, jestli jsou tyto informace správné a jak případně zdůvodním. U samotné množiny R předpokládám, že infimum ani supremum nemá, protože není zdola ani shora omezená.
Budu rád, pokud sem někdo napíše svůj pohled na věc.
Offline
- (téma jako vyřešené označil(a) Matthew19)
#2 28. 10. 2018 16:31
Re: Infimum a supremum R, N a prázdné množiny
↑ Matthew19: Nie su spravne. Aku literaturu pouzivas?
Offline
#3 28. 10. 2018 17:03
Re: Infimum a supremum R, N a prázdné množiny
↑ vlado_bb: U prázdné množiny jsem čerpal z článku na wikipedii:
https://cs.wikipedia.org/wiki/Pr%C3%A1z … o%C5%BEina
To, že nekonečno je supremem N jsem se dočetl tady:
http://math.feld.cvut.cz/mt/txtb/1/txc3ba1b.htm
Mohl bys mi tedy říct, jak to je správně?
Offline
#4 28. 10. 2018 17:27 — Editoval vlado_bb (28. 10. 2018 17:39)
Re: Infimum a supremum R, N a prázdné množiny
↑ Matthew19: Spravne je mat papierovu knihu alebo skripta, v nich najst definiciu suprema a infima a pochopit ich. Pokial ide o N, to infimum je teda ake? Ak chapes definiciu infima, budes to vediet.
Offline
#5 28. 10. 2018 18:23
Re: Infimum a supremum R, N a prázdné množiny
↑ vlado_bb: Definici suprema a infima znám a do teď jsem si myslel, že ji i chápu. U prázdné množiny si to ale moc nedokážu představit a odůvodnit. Myslel jsem, že infimem N je minus nekonečno, protože jsem se dočetl, že supremem je plus nekonečno...
Offline
#6 28. 10. 2018 18:30
Re: Infimum a supremum R, N a prázdné množiny
↑ Matthew19: V tom pripade definiciu infima nechapes. Skus overit ci ju  splna.
splna.
Offline
#7 29. 10. 2018 17:57 — Editoval MichalAld (29. 10. 2018 18:02)
Re: Infimum a supremum R, N a prázdné množiny
↑ vlado_bb:
A jak je to s tou prázdnou množinou ? Podle mého "selského rozumu" by žádné infimum ani supremum mít neměla...třeba jen proto, že prázdná množina může být "prázdná množina čehokoliv", co nijak s čísly nesouvisí.
Na té odkazované wiki je použitý termín "prázdná množina reálných čísel", to se opravdu používá ?
Offline
#8 29. 10. 2018 17:58
Re: Infimum a supremum R, N a prázdné množiny
Matthew19 napsal(a):
↑ vlado_bb: Definici suprema a infima znám a do teď jsem si myslel, že ji i chápu. U prázdné množiny si to ale moc nedokážu představit a odůvodnit. Myslel jsem, že infimem N je minus nekonečno, protože jsem se dočetl, že supremem je plus nekonečno...
Možná také nechápeš, co jsou "přirozená čísla"...
Offline
#9 29. 10. 2018 18:12
Re: Infimum a supremum R, N a prázdné množiny
MichalAld napsal(a):
↑ vlado_bb:
A jak je to s tou prázdnou množinou ? Podle mého "selského rozumu" by žádné infimum ani supremum mít neměla...třeba jen proto, že prázdná množina může být "prázdná množina čehokoliv", co nijak s čísly nesouvisí.
Na té odkazované wiki je použitý termín "prázdná množina reálných čísel", to se opravdu používá ?
No minimálně jednou už to použito bylo.:-)
A pokud ti opravdu není jasné, proč má prázdná množina inf a sup taková, jaká má, tak si tu definici inf a sup taky ještě jednou prostuduj.;-)
Offline
#10 29. 10. 2018 20:13
Re: Infimum a supremum R, N a prázdné množiny
MichalAld napsal(a):
↑ vlado_bb:
Na té odkazované wiki je použitý termín "prázdná množina reálných čísel", to se opravdu používá ?
Dobra ukazka toho, ze Wikipedia nie je zdroj pre studium.
Offline
#11 29. 10. 2018 22:06
Re: Infimum a supremum R, N a prázdné množiny
vlado_bb napsal(a):
MichalAld napsal(a):
↑ vlado_bb:
Na té odkazované wiki je použitý termín "prázdná množina reálných čísel", to se opravdu používá ?Dobra ukazka toho, ze Wikipedia nie je zdroj pre studium.
Wikipedia naozaj nieje dobry zdroj studia, lebo je to encyklopedia a nie ucebnica. Ale je velmi dobry zdroj ked ide o referencie, lebo je to encyklopedia ...
informacie v nej su skor spravne ako nespravne, tlacena ucebnica ma obvykle vacsiu hustotu chyb a nepresnosti, lebo ju nemoze niekto neustale editovat.
prazdna mnozina je prazdna mnozina cohokolvek a teda pokojne aj realnych cisel.
btw. 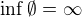 a
a 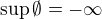 je obvyklou sucastou definicie pojmov infimum a supremum ak sa definuju v kontexte realnej analyzy co je typicky prvy predmet v ktorom sa s nimi student stretne.
je obvyklou sucastou definicie pojmov infimum a supremum ak sa definuju v kontexte realnej analyzy co je typicky prvy predmet v ktorom sa s nimi student stretne.
samozrejme sa da ta definicia urobit aj bez nej ... to uz je tazky zivot matematika, ze si musi davat pozor na rozne neekvivalentne definicie rovnakych pojmov.
Offline
#12 29. 10. 2018 22:40
Re: Infimum a supremum R, N a prázdné množiny
Ahoj ↑ Brano:,
Dovolim si doplnit tvoj prispevok.
Definicia sup a inf sa rozlisuje pokial pracujeme v 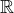 alebo
alebo 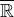 (komplete
(komplete 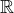 ).
).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 29. 10. 2018 23:04
Re: Infimum a supremum R, N a prázdné množiny
↑ Stýv:
No já se snažím...
Našel jsem třeba takovouto definici.
Jenže pořád je tam množina X a její podmožina Y, u které hledáme to infimum. Pokud bude X množina reálných čísel a Y prázdná množina, tak vyjde co říkáš.
Ale co když nebude X = R, co když bude X třeba jen interval, <0, 1>. Prázdná množina je i jeho podmožinou (prázdná množina je podmožinou všeho, né ?). Potom to nekonečno určitě nebude (infimum musí být prvek z množiny X).
Prostě mi připadá, že představa infima prázdné množiny je divná, že výsledek nezávisí na té prázdné množině, ale na té její nadmožině (jestli se to tak nazývá). Do jisté míry to na ní závisí i jindy, ale jen jako takové omezení. Jinak je ale infimum nějaké množiny vlastností té množiny. Zatímco u prázdné množiny né, tam je to čistě vlastností té nad ní. Proto mi ten pojem přijde divný...
Já teda vlastně nechápu ani to nekonečno jakožto prvek množiny R...myslel jsem, že R neobsahuje nekonečna...ale to s tím předchozím asi nesouvisí.
Offline
#15 29. 10. 2018 23:15
Re: Infimum a supremum R, N a prázdné množiny
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 30. 10. 2018 08:13
Re: Infimum a supremum R, N a prázdné množiny
Pro množinu všech reálných čísel rozšířenou o ta dvě nekonečna se někdy používá zde uvedený symbol  , ale lepší prý je používat symbol
, ale lepší prý je používat symbol 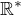 , protože pruh se používá pro uzávěr množiny.
, protože pruh se používá pro uzávěr množiny.
Myslím, že pro prázdnou množinu musíme definovat infimum a supremum explicitně, protože jinak se tyto pojmy definují pomocí největší dolní a nejmenší horní závory množiny. Množinou dolních nebo horních závor prázdné množiny je celá množina  , tam žádný nejmenší ani největší prvek není.
, tam žádný nejmenší ani největší prvek není.
Offline
#18 30. 10. 2018 08:18
Re: Infimum a supremum R, N a prázdné množiny
Prostě, nejjednodušší by bylo říct, že supremum a infimum prázdné množiny odpovídá minimu a maximu té její nadmnožiny (a případně proč) .... a pak teprve, že pro R to neexistuje a pro R* je to plus minus nekonečno. A každý (nebo teda aspoň já) by to hned pochopil.
Offline
#19 30. 10. 2018 09:10
Re: Infimum a supremum R, N a prázdné množiny
↑ MichalAld: No a to je právě to důležitý si uvědomit, že sup/inf závisí na "kontextu", tj. na té nadmnožině. Neplatí to jenom pro prázdnou množinu. Např. neomezené množiny nemají sup v R, ale mají sup v R*. Nebo ještě "lepší" příklad: jaképak je např. 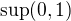 v množině
v množině ![kopírovat do textarea $(0,1)\cup\[2,3\]$](/mathtex/9e/9e4130f67b6e7107e515ac79968f6edb.gif) ?;-)
?;-)
Offline
#20 30. 10. 2018 12:21 — Editoval jarrro (30. 10. 2018 12:22)
Re: Infimum a supremum R, N a prázdné množiny
↑ MichalAld:Obyčajne sa definuje supremum resp. infimum podmnožiny posetu ako najmenšie horné resp. najväčšie dolné ohraničenie. Množina horných resp. dolných ohraničení prázdnej množiny je celý poset, lebo
Výroky  a
a 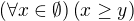 platia pre všetky
platia pre všetky  z posetu
z posetu
Teda infimum je najväčší prvok posetu a supremum najmenší (v prípade 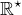 sú to
sú to 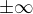 )
)
MATH IS THE BEST!!!
Offline
#21 30. 10. 2018 12:40
Re: Infimum a supremum R, N a prázdné množiny
↑ MichalAld:Mnozina realnych cisel je v analyze rozsirena o plus a minus nekonecno hlavne kvuli limitam.Nekonecna nejsou bezne brana jako realna cisla,protoze nesplnuji stejna pravidla jako cisla,netvori Abelovu grupu. 0 krat nekonecno neni nekonecno apod.Ale v limitach a nasledne u prubehu funkce s nimi musis jako s cisly pracovat,maji vsak sva pravidla. Vsimni si posledniho prikladu v limit maratonu. I zde musis limitu pocitat,ze si uvedomis ,ze n! je nejvyssi mocnina a vydelis citatele i jmenovatele n!.Rozhodne ale nemuzrs pouzit uvahu,ze kdyz limita podilu je 1 ,tak limita rozdilu je 0. Mej se hezky.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#22 31. 10. 2018 13:21
Re: Infimum a supremum R, N a prázdné množiny
Jen dodám, že hodnota suprema a infima prázdné množiny závisí na volbě její nadmnožiny a uspořádání.
- pro 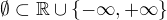 je
je 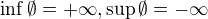
- pro 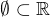 ani jeden z výrazů
ani jeden z výrazů  neexistují
neexistují
- pro 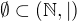 (přirozená čísla uspořádaná dělitelností) máme
(přirozená čísla uspořádaná dělitelností) máme 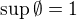 a
a 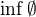 neextuje
neextuje
- pro 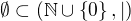 je
je 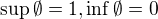
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Infimum a supremum R, N a prázdné množiny (TOTO TÉMA JE VYŘEŠENÉ)

