Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 12. 2017 18:38
Pravděpodobnost – tombola
Zdravím všechny,
měl bych tu dotaz ohledně pravděpodobnosti při losování tomboly.
Mějme následující situaci: celkem bylo prodáno 200 lístků, k výhře je 5 cen 1. kategorie a 15 cen 2. kategorie. Já jsem si koupil 8 lístků.
1) Jaká je pravděpodobnost, že vyhraji 2 ceny 1. kategorie?
2) Jaká je pst, že vyhraju 1 cenu 1. kategorie a 1 cenu 2. kat.?
Pokus o výpočet:
ad 1) 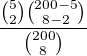
ad 2) 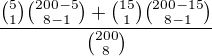
Ale nezdá se mi to správně. Mělo by platit, že součet pstí vylosování dvou cen 1. kat., dvou 2. kat a dvou odlišných je stejná jako pst vylosování 2 nějakých cen, že jo? To mi ale nevychází. Vylosování dvou nějakých cen bych bral jako: 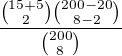
Díky za pomoc či naznačení.
Offline
- (téma jako vyřešené označil(a) krauva)
#2 27. 12. 2017 22:38
Re: Pravděpodobnost – tombola
↑ krauva:
Dobrý den.
Řekl bych, že odpověď na 1. dotaz je v pořádku, pokud jej lze chápat tak, že kromě právě dvou cen první kategorie může být ve vaší výhře 0 - 6 cen druhé kategorie.
Odpověď na druhý bych spíše viděl takto: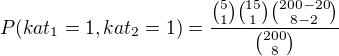
Nevím proč by měla platit rovnost pravděpodobností podle dalšího odstavce.
Pokud se tedy nemýlím.
Offline
#5 03. 11. 2018 11:19
Re: Pravděpodobnost – tombola
↑ krauva:
Ahojte, napadl mě ještě jeden dotaz :). A sice, jaká je pravděpodobnost, že vyhraju alespoň jednu cenu (nějakou), tedy 1 a více?
Samozřejmě mě napadlo využít pravděpodobnost opačného jevu (nevyhraju žádnou), tj pak by pravděpodobnost byla: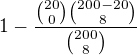 ,že?
,že?
Dá se to ale spočítat, aniž bych použil opačný jev? Napadla mě následující úvaha, z 20 výherních losů si vyberu jeden a zbylých 7 si vyberu ze 199 ostatních, číslo ale nesedí.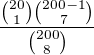
Lze tedy pravděpodobnost spočítat takovýmto způsobem?
Díky za rady.
Offline