Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 06. 11. 2018 16:03
Re: Parciální diferenciální rovnice
Frankie napsal(a):
Ten druhý průběh, ve kterém se uvažuje i prostorový náboj okolo té koule, má vyjít z této rovnice - Poissonova rovnice:
Bez záruky, ale až po vztah
by měl být postup stejný, jen na pravé staně bude namísto nuly ta 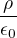
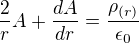
Možná to půjde vyřešit metodou variace konstant. Musí se tam ovšem dosadit nějaká konkrétní funkce průběhu nábojové hustoty.
Ale už je to dlouho, co jsem řešil nějaké jiné dif. rovnice, než lineární, takže se do toho raději nebudu pouštět, a nechám to na někom jiném.
Online
#27 07. 11. 2018 17:59
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Parciální diferenciální rovnice
No jo, on to má vlastně zapsané už v téhle formě. Já jsem si představoval, že bych musel řešit rovnici s Laplacovým operátorem...
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#28 07. 11. 2018 22:45
Re: Parciální diferenciální rovnice
To se řešit nedá. Leda numericky. Nebo možná v nějakých velmi speciálních případech.
Trik s použitím cylindrických nebo sférických souřadnic je jeden z mála způsobů, jak se k nějakému výsledku dopracovat. Za předpokladu, že máme takto symetrickou také fyzikální situaci. (nakonec i černá díra v teorii gravitace je vypočítána tímhle trikem).
Tím, že zavedeme sférické souřadnice ve sféricky symetrické situaci nám derivace podle dvou proměnných vypadnou (podle těch dvou úhlů - protože v jejich směru se nic nemění, tudíž jsou nulové) a zůstanou jen derivace dle r. LaPlaceův operátor ve sférických souřadnicích je sice o dost složitější než v kartézských, ale vynaložená námaha se vyplatí.
I když - všechny tyhle úlohy postavené na symetrii lze řešit pomocí Gaussovy věty - a se středoškolskou matematikou (tj bez nějakých diferenciálních rovnic).
Online
#29 10. 11. 2018 01:03
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Parciální diferenciální rovnice
To se řešit nedá.
Aha. 🙂 Je dokázáno, že se to obecně analyticky řešit nedá?
I když - všechny tyhle úlohy postavené na symetrii lze řešit pomocí Gaussovy věty - a se středoškolskou matematikou (tj bez nějakých diferenciálních rovnic).
My zatím nevíme, jaká bude ta hustota náboje. (Resp. já to nevím.) Viz
↑↑ KennyMcCormick:
Nenapadá mě žádný důvod předpokládat, proč by "oblak stínících částic" měl by být kolem nabité koule jiný než kolem nabitého bodu.
Protože kdyby to byl jeden bod, byly by stínící částice i uvnitř myšlené koule, zatímco v případě skutečné koule není uvnitř koule nic. Takže stínící částice mimo myšlenou kouli by měly cítit menší náboj v případě bodu než v případě skutečné koule, a tudíž by jich tam mělo být méně.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#30 10. 11. 2018 13:22 — Editoval Frankie (10. 11. 2018 13:28)
Re: Parciální diferenciální rovnice
KennyMcCormick napsal(a):
To se řešit nedá.
Aha. 🙂 Je dokázáno, že se to obecně analyticky řešit nedá?
I když - všechny tyhle úlohy postavené na symetrii lze řešit pomocí Gaussovy věty - a se středoškolskou matematikou (tj bez nějakých diferenciálních rovnic).
My zatím nevíme, jaká bude ta hustota náboje. (Resp. já to nevím.) Viz
↑↑ KennyMcCormick:Nenapadá mě žádný důvod předpokládat, proč by "oblak stínících částic" měl by být kolem nabité koule jiný než kolem nabitého bodu.
Protože kdyby to byl jeden bod, byly by stínící částice i uvnitř myšlené koule, zatímco v případě skutečné koule není uvnitř koule nic. Takže stínící částice mimo myšlenou kouli by měly cítit menší náboj v případě bodu než v případě skutečné koule, a tudíž by jich tam mělo být méně.
Hustoty nábojů si mám všechny zvolit dle libosti. Mám si úlohu zjednodušit. Jde jen o vyřešení té Poissonovy rovnice pro ten potenciál, jak psal MichalAld - tedy především o aplikaci matematických postupů.
Offline
#31 11. 11. 2018 07:47 — Editoval KennyMcCormick (25. 11. 2018 11:59)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Parciální diferenciální rovnice
Já jsem myslel, že konkrétní průběh té exponenciálně klesající hustoty bude do určité míry omezený fyzikálními zákony, ale jestli si skutečně můžeš zvolit hustoty náboje úplně jakkoliv (což se mi zdá divné, ale jestli sis jistý), tak si zvol např.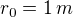 (poloměr koule)
(poloměr koule) (hustota kladného náboje na povrchu koule) a
(hustota kladného náboje na povrchu koule) a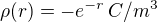 , kde
, kde  (hustota záporného náboje v okolí koule).
(hustota záporného náboje v okolí koule).
Pokud máš pouze nabitou kouli s prostorovým nábojem kolem ní a chceš, aby ji stínil, musí mít opačné znaménko (tedy něco jiného, než píše tvůj text), jak jsem psal tady:
↑↑ KennyMcCormick:
Není možné, aby dodatečný kladný náboj zeslabil existující kladný náboj, protože náboje stejného znaménka se zesilují.
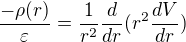


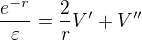
Substituce: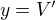
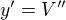
Dostáváme rovnici: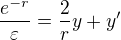
Najdeme řešení této rovnice:
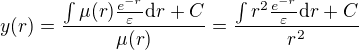
Abychom získali 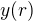 , vyřešíme integrál
, vyřešíme integrál 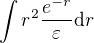 :
:
Použijeme metodu per partes, označíme  a
a 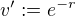 , tj.
, tj. 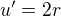 a
a 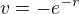 . Odtud
. Odtud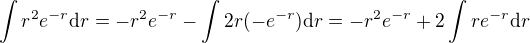 .
.
Vypočteme stranou integrál 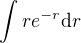 opět metodou per partes, označíme
opět metodou per partes, označíme 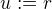 a
a 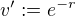 , tj.
, tj. 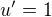 a
a 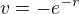 . Dostaneme
. Dostaneme .
.
Dosadíme do předchozího integrálu a dostaneme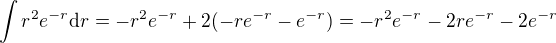 .
.
Dosadíme do integrálu předtím a získáme: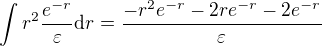
Dosadíme do rovnice pro 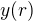 , čímž dostáváme
, čímž dostáváme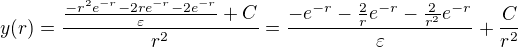 .
.
Teď dosadíš do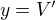 , čímž získáš
, čímž získáš  .
.
Budeš mít 2 konstanty, které určíš ze dvou okrajových podmínek.
Edit: Chybná část skryta.
Edit: Oprava
 na
na 
Edit2: Ty okrajové podmínky jsem samozřejmě napsal špatně - je to intenzita (tj.
 ), která je blízko u povrchu rovna intenzitě ve vzdálenosti 1 m od bodového náboje, ve kterém je soutředěný náboj nacházející se na povrchu koule.
), která je blízko u povrchu rovna intenzitě ve vzdálenosti 1 m od bodového náboje, ve kterém je soutředěný náboj nacházející se na povrchu koule. Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#32 12. 11. 2018 17:05
Re: Parciální diferenciální rovnice
KennyMcCormick napsal(a):
To se řešit nedá.
Aha. 🙂 Je dokázáno, že se to obecně analyticky řešit nedá?
Já mám dokonce pocit, že pro obě rovnice existuje obecné řešení, ale není z něho zvláštní užitek. Pro Poissonovu rovnici lze napsat řešení s využitím Greenových funkcí, není to ale v důsledku nic jiného, že pro každý bod, kde je nenulová hustota náboje spočítáme klasický Coulombovský potenciál k/r a v každém bodě prostoru sečteme příspěvky od všech dílčích nábojů.
Ale dělat to analyticky - podle mě z toho žádný užitek není. Další problém, na který v praxi narazíme je, že né vždy známe polohu nábojů. Reálné situace zpravidla neobsahují pevně uložené náboje, nýbrž různě natvarované vodiče, a tady nám Poissonova rovnice moc nepomůže.
Na to je zase dobrá ta LaPlaceova. S tím, že se to řeší jen mezi těmi vodiči - a povrch vodiče se tam zadává jako okrajová podmínka.
Obecné řešení Laplaceovy rovnice existuje určitě také. Mám dokonce pocit, že každá "slušná" komplexní funkce f(x + iy) je jejím řešením. ("slušná" se myslím v komplexní analýze nazývá holomorfní). Stačí jen z té celkem slušně velké zásoby holomorfních funkcí vybrat tu, která nám zároveň splní okrajové podmínky. Ale nevím, jestli se o to někdy někdo takto snažil.
Mnohem jednodušší je to asi spočítat numericky. Zkoušel jsem si to i na střední škole - samozřejmě v jednoduchých situacích. Stačí si v prostoru stanovit pár bodů (no, mělo by jich být co nejvíc, žejo) a pak opakovaně počítat, že v každém bodě je potenciál rovný průměru z těch okolních bodů. Tak dlouho, dokud to vykazuje nějaké změny.
Je to hloupá metoda, ale člověk nemusí být raketový inženýr, aby si spočítal nějaké rozložení elektrického pole. A dá se to i experimentálně ověřit - jednoduchým trikem, že elektrické pole se řídí stejnou rovnicí jako proudové pole. Takže když se vezme navlhčený písek, a dají se do něj stejné elektrody, tak pole potenciálu je také stejné. A kouskem drátu zapíchnutým do písku jej lze hezky měřit - což je u potenciálu ve vakuu téměř neproveditelné.
Online
#33 13. 11. 2018 04:16
Re: Parciální diferenciální rovnice
↑ KennyMcCormick:
Mohl by si mi prosím trošku objasnit, co se v tomto kroku vlastně dělalo ?
Dostáváme rovnici: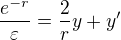
Najdeme řešení této rovnice:
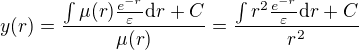
Vůbec se tím nedokážu prokousat. Tu rovnici neumím vyřešit. Vždy jsme řešili jen jednoduché typové úlohy, takže mám problém s aplikací do praxe.
Offline
#34 13. 11. 2018 06:41
Re: Parciální diferenciální rovnice
↑ Frankie:↑ KennyMcCormick:
K těm hodnotám... Bylo mi právě řečeno, že si to mám "vhodně" zvolit. Respektive zkusit to nějak zjednodušit tak, abych zhruba vykreslil ty charakteristiky průběhu potenciálu, co jsem zde již ukazoval.
K dořešení této rovnice.. Delší dobu se tady v tom motám a marně se snažím dohnat základy řešení dif. rovnic. Kdyby jsi měl chuť a čas to ještě dokončit, byl bych ti vděčný.
Offline
#35 13. 11. 2018 08:36 — Editoval MichalAld (13. 11. 2018 08:36)
Re: Parciální diferenciální rovnice
↑ Frankie:
Jde to řešit i metodou "variace konstanty". Pokud víme, že řešení rovnice bez pravé strany 
je 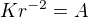
tak řešení rovnice s pravou stranou 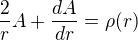
nalezneme tak, že tu konstantu K z předchozího řešení budeme považovat za funkci, tj K(r).
je 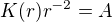
To dosadíme do rovnice, takže dostaneme (po zderivování)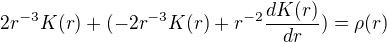
Ty dva členy se nám hezky odečtou, a zůstane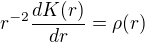


Píši to ovšem dost ve spěchu, takže tam může být nějaká chyba - ale zdá se, že to vychází stejně jako u ↑ KennyMcCormick:
Ta funkce 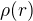 může být úplně libovolná (rozumná), takže pokud si ji můžeš zvolit, tak si ji zvol tak, aby se ti integrál hezky počítal (a vyšel konečný, pokud možno).
může být úplně libovolná (rozumná), takže pokud si ji můžeš zvolit, tak si ji zvol tak, aby se ti integrál hezky počítal (a vyšel konečný, pokud možno).
Online
#36 13. 11. 2018 09:29 — Editoval Frankie (13. 11. 2018 09:32)
Re: Parciální diferenciální rovnice
↑ MichalAld:
Ohledně té volby funkce prostorového náboje. Jako rozumnou mi vedoucí doporučil použití jednoduché 1/r.
Offline
#37 13. 11. 2018 09:52
Re: Parciální diferenciální rovnice
Z hlediska počítání je to OK, ale problém je, že integrál musí konvergovat - tj musí dávat konečnou hodnotu i při integraci přes celý prostor. Jinak řečeno - převážná část náboje se musí nacházet v okolí té kuličky, kolem které to řešíš. Potenciál musí vycházet konečný i v nekonené vzdálenosti. To je potřeba ověřit.
Online
#38 13. 11. 2018 15:23
Re: Parciální diferenciální rovnice
↑↑ Frankie:
Rozoberiem trochu postup od ↑↑ kerajs:, je to vseobecne casto uzitocny postup pri hladani vlastnych funkcii operatoru v nekartezskych suradniciach.
Prvy krok je uvedomit si ze mozeme zahodit 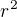 (samozrejme v bode
(samozrejme v bode  nema rovnica zmysel tak ci tak).
nema rovnica zmysel tak ci tak).
Druhy krok je vyuzit 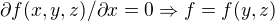 bez ohladu na to co su
bez ohladu na to co su  . Takze pre tento pripad: vnutro zatvorky je na
. Takze pre tento pripad: vnutro zatvorky je na  nezavisle explicitne.
nezavisle explicitne.
Ostava 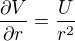 kde
kde  nezavisi explicitne na
nezavisi explicitne na  , ale moze na inych suradniciach. Ak su tieto suradnice povazovane za nezavisle na
, ale moze na inych suradniciach. Ak su tieto suradnice povazovane za nezavisle na  , potom skutocne staci zintegrovat podla
, potom skutocne staci zintegrovat podla  .
.
Offline
#39 14. 11. 2018 03:19
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Parciální diferenciální rovnice
A dá se to i experimentálně ověřit - jednoduchým trikem, že elektrické pole se řídí stejnou rovnicí jako proudové pole.
Řídí se jakékoliv proudové pole Poissonovou rovnicí?
↑ Frankie:
Tu rovnici neumím vyřešit.
To nevadí, protože řešení jsem ti tam napsal já. 🙂
Vůbec se tím nedokážu prokousat.
Vysvětlím ti to. Pokud máš diferenciální rovnici ve tvaru a označíme
a označíme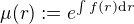 , je řešení rovnice
, je řešení rovnice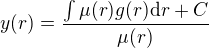 .
.
Je zbytek toho, co jsem napsal, jasný?
↑ Frankie:
Ohledně té volby funkce prostorového náboje. Jako rozumnou mi vedoucí doporučil použití jednoduché 1/r.
Tak do té rovnice místo 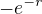 dosaď
dosaď  a uprav výpočet odpovídajícím způsobem. Kdybys potřeboval s výpočtem potenciálu ještě poradit, dej vedět.
a uprav výpočet odpovídajícím způsobem. Kdybys potřeboval s výpočtem potenciálu ještě poradit, dej vedět.
Taky bude potřeba, aby sis změnil povrchový náboj ze 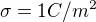 na nějaké záporné číslo (např.
na nějaké záporné číslo (např. 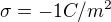 ).
).
↑ MichalAld:
Potenciál musí vycházet konečný i v nekonečné vzdálenosti. To je potřeba ověřit.
To je vlastně taky pravda.
↑ Xellos:
Rozoberiem trochu postup od ↑↑ kerajs:
Btw, teď už počítáme Poissonovu rovnici. 🙂
Prvy krok je uvedomit si ze mozeme zahodit
(samozrejme v bode
nema rovnica zmysel tak ci tak).
Vidíš, to jsem si vůbec neuvědomil - v té fyzikální situaci, kterou řeší, je potenciál v  nějaká konstanta, takže jsem ani nezaregistroval, že jeho rovnice to nepřipouští.
nějaká konstanta, takže jsem ani nezaregistroval, že jeho rovnice to nepřipouští.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#40 14. 11. 2018 13:18
Re: Parciální diferenciální rovnice
KennyMcCormick napsal(a):
A dá se to i experimentálně ověřit - jednoduchým trikem, že elektrické pole se řídí stejnou rovnicí jako proudové pole.
Řídí se jakékoliv proudové pole Poissonovou rovnicí?
Ani né tak Poissonovou, jako Laplaceovou - Poissonova - to by fyzikálně znamenalo, že jsou tam spojitě rozložené zdroje proudu (podobně jako náboj v el. poli)
Jakékoliv asi né. Obecně platí Maxwellovy rovnice, v prostředí bez nábojů a ve statických případech jako
rot E = 0, div E = 0, z první rovnice plyne přímo E = - grad 
a k tomu materiálová rovnice 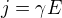
Abychom dostali LaPlaceovu rovnici, musí to  , tak řečeno komutovat s diverenciálními operátory.
, tak řečeno komutovat s diverenciálními operátory.
Což je určitě splněno, když prostředí je homogenní (v prostoru i čase), izotropní (nezávislé na směru) a lineární.
Zkrátka, když je vodivost prostě konstanta, nezávislá na čemkoliv (když platí Ohmův zákon).
Možná lze nějak řešit i ten případ anizotropních materiálů - to by pak byla vodivost popsána tenzorem - ale s tím se u vodivosti většinou nesetkáváme (narozdíl od permitivity).
Je také možné, aby tyto podmínky platily jen pro určité podoblasti (jako že v části prostoru bude vodivost nějaká a jinde jiná) - pak se řeší rovnice v každé oblasti zvlášť a složí se pomocí okrajových podmínek.
V ostatních případech (nelineární závislost proudu na napětí, nehomogenní či časově proměnná vodivost) už Laplaceova rovnice neplatí.
Proud také ovlivňuje magnetické pole, takže je ještě nutné, aby byly proudy malé (a magnetické pole bylo možné zanedbat).
Online
#41 14. 11. 2018 23:01
Re: Parciální diferenciální rovnice
↑ MichalAld:
Máš nějakou představu o řešení ? Já vůbec netuším. Bez konzultace a doučení matiky tohle nedám. Jestli by si věděl, jakým směrem se dát, byl bych moc rád. Už mám asi jen 14 dní. Pak už je konec.
Offline
#42 14. 11. 2018 23:06 — Editoval Frankie (14. 11. 2018 23:21)
Re: Parciální diferenciální rovnice
Pakliže by se někdo našel, rád bych problematiku nějak intenzivněji řešil. Času již moc nemám, tak zkusím vše. Nemám matematické znalosti na to, tohle vyřešit, protože k výkonu své praxe to již delší dobu nepotřebuji a kromě téhle úlohy po nás na vysoké škole aplikaci matematiky nikdo nechtěl, takže bych klidně poskytl nějakou finanční náhradu za čas strávený s řešením této úlohy.
Úlohou totiž není tak ani důkladné prověření znalosti fyziky. Ale hlavě aplikování matematiky. Jak jsem již psal - vše si mohu ulehčit v rámci možností. Vše zvolit. VŠECHNO SI MOHU ZJEDNODUŠIT.
Offline
#43 15. 11. 2018 02:53 — Editoval KennyMcCormick (15. 11. 2018 02:54)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Parciální diferenciální rovnice
Já jsem ti tady ↑ KennyMcCormick: odpověděl na otázku, co znamená to, co jsem napsal. Takže, kam až to chápeš teď? Který řádek mého řešení je poslední řádek, kterému ještě rozumíš?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline

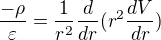
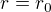 bude roven potenciálu ve vzdálenosti 1 m od bodového náboje, ve kterém je soutředěný náboj nacházející se na povrchu koule.
bude roven potenciálu ve vzdálenosti 1 m od bodového náboje, ve kterém je soutředěný náboj nacházející se na povrchu koule.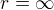 je nulový.
je nulový. je stejný jako ve vzdálenosti
je stejný jako ve vzdálenosti