Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 12. 11. 2018 14:48 — Editoval Rumburak (12. 11. 2018 14:54)
Re: Množina
↑ šidlo:
Ahoj.
Především je vhodné uvědomit si, co znamená tvrzení, že množina  je konečná resp. nekonečná.
je konečná resp. nekonečná.
Definice říká, že:
Množina  je konečná právě tehdy, když pro libovolné zobrazení
je konečná právě tehdy, když pro libovolné zobrazení 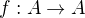 , které je prosté
, které je prosté
(tj. splňuje podmínku  ) , platí
) , platí  .
.
O množině, která není konečná, říkáme, že je nekonečná. Takže:
Množina  je nekonečná právě tehdy, když existuje zobrazení
je nekonečná právě tehdy, když existuje zobrazení 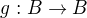 , které je prosté a
, které je prosté a
při tom 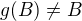 .
.
Je zřejmé, že
(1) prostý obraz konečné množiny je konečná množina, tutíž také prostý obraz nekonečné mmnožiny
je nekonečná množina,
(2) "zvětšením" nekonečné množiny tím, že do ni přidáme další prvky, dostaneme množinu, které bude
rovněž nekonečná, analogicky "ubráním" prvků z konečné množiny dostaneme množinu rovněž
konečnou.
V čem je konkretní problém ?
Offline
#4 15. 11. 2018 21:39
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: Množina
↑ Rumburak:
Ahoj, nejsem si jist, zda na střední škole mají definovány nekonečné množiny takto precizně a nebo zda je chápou poněkud "intuitivněji".
"Máte úhel beta." "No to nemám."
Offline
#5 16. 11. 2018 06:28 — Editoval johnyk (16. 11. 2018 06:39) Příspěvek uživatele johnyk byl skryt uživatelem johnyk. Důvod: kecám tam blbosti
#6 16. 11. 2018 07:07
- misaH
- Příspěvky: 13459
Re: Množina
↑ johnyk:
Vieš čo, nemáš pravdu a nemýľ tu ľudí.
Samozrejme, že záleží na tom, o akej množine je reč.
To, čo tvrdíš napríklad pre interval tvorený z prirodzených čísel neplatí.
Prečítaj si príspevok hneď pod zadaním od autora krakonoš.
Niečo je v ňom nepochopiteľné?
Offline
#8 16. 11. 2018 09:32 — Editoval vlado_bb (16. 11. 2018 09:35)
Re: Množina
↑ krakonoš: A vy viete, co je to "mnozina zadana mnozinou"? Co je mnozina zadana mnozinou 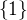 ? Alebo mnozinou vsetkych psuedometrik v
? Alebo mnozinou vsetkych psuedometrik v  .
.
Offline
#9 16. 11. 2018 10:06 — Editoval krakonoš (16. 11. 2018 10:16)
Re: Množina
↑ vlado_bb:
Zhruba si pamatuji,ze mnozina vsech mnozin neni mnozina.Prednasky z teorie mnozin jsem absolvovala pred vic jak 30 lety.Tady jde o stredoskolsky priklad,tak myslim,ze to bylo mysleno,jak pisu.Asi nema cenu se se stredoskolaky ani bavit o tom ,ze mezi intervalem a realnou primkou existuje vzajemne jednoznacne zobrazeni.
Casto se tu setkavame i s nepresnym vyjadrenim zadavatele.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#10 16. 11. 2018 10:20
Re: Množina
↑ krakonoš: Z vasej vety "Je zde rec o mnozine ZADANE INTERVALEM.,nikoli zda sam interval obsahuje konecne ci nekonecne bodu." sa zda, ze viete, co je to mnozina zadana mnozinou. Pytam sa vas na vase vlastne tvrdenie, na nic ine.
Offline
#11 16. 11. 2018 11:03
Re: Množina
↑ vlado_bb:
Mnozina zadana mnozinou je podle me blbost.Zde ale byla rec o intervalu,otazka mohla byt lepe formulovana,coz nekdy nedokaze ani Cermat,natoz laici.Vzdy musime vystihnout,o co lidem jde.
Navic slovo interval vyjadruje i neco dalsiho.U mnoziny nezalezi na poradi prvku.A jak se divat na treba posloupnost? Rozhodne ne jako na mnozinu!
Zde ve foru se nedavno nekdo ptal na logaritmicke rovnice,mel totalni zmatek v pojmech umocneni xka a celeho logaritmu,a log x rikal koren a mluvil o jeho zapornosti.Zde ve foru mu bylo odpovezeno pomoci pojmu hlavni vetev logaritmu,a ze logaritmus zaporneho cisla je komplexni cislo.Tento logaritmus vzdy ale znacime velkym pismenem,zde po celou dobu byla rec o logaritmu s l.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#12 16. 11. 2018 11:55 — Editoval misaH (16. 11. 2018 11:56)
- misaH
- Příspěvky: 13459
Re: Množina
Intervaly používáme i v běžné mluvě, například „za nesprávnou barvu svých očí můžete od Evropské unie dostat pokutu v rozmezí deset až dvacet tisíc korun“. V příkladu je použito slovo „rozmezí“, ale matematicky vzato se jedná o interval. Teď ale nastávají zrádné otázky: můžete dostat pokutu přesně deset tisíc korun nebo se tam krajní hodnota rozmezí nepočítá? Jak moc jemně si mohu pokutu vybírat? Mohu dát pokutu 18 541,97 korun? Nebo mohu škálovat například pouze po stovkách? Tj. buď 18 500 nebo 18 600?Vše řeší matematický zápis. Při něm musíme říci dvě podstatné věci: v jaké množině se pohybujeme (v kontextu příkladu – stovky? Tisíce? Jednotky korun?) a jestli do intervalu spadají i krajní body (mohu dostat pokutu právě deset nebo dvacet tisíc?).Dobrá zpráva je, že v drtivé většině případů v matematice chceme, aby interval pracoval s množinou reálných čísel, takže pokud narazíte na interval bez specifikace množiny, jedná se jistě o reálná čísla.
Toľko matematika.cz...
Offline

