Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 11. 2018 17:25
Obor pravdivosti výrokovej formy
Viete mi prosim niekto povedat ako vyriesit tento priklad? Treba najst obor pravdivosti vyrokovej formy:
5 ≤ 4|x − 1| + |2 − 3x|
definovanej nad oborom reálnych čísel. Treba dokazat, že naše riešenie je správne.
V dôkaze sa doporučuje využiť niektorú z nasledujúcich vlastností absolútnej hodnoty reálneho čísla:
∀x∀y |xy| = |x||y|
∀x∀y(y ≤ |x| ↔ y ≤ x ∨ y ≤ −x)
∀x∀y(|x| ≤ y ↔ x ≤ y ∧ −x ≤ y)
Offline
#4 17. 11. 2018 18:12
Re: Obor pravdivosti výrokovej formy
Riešenie tej nerovnice je : (- , 1/7>
, 1/7>  <11/7,
<11/7,  )
)
Problem je ze neviem ako pouzit jednu z tych viet ako dokaz. Napr. ked pouzijem tuto:
∀x∀y(y ≤ |x| ↔ y ≤ x ∨ y ≤ −x)
tak dostanem:
5  4(x-1) + (2-3x)
4(x-1) + (2-3x)  5
5  - [4(x-1) + (2-3x)]
- [4(x-1) + (2-3x)] 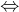 5
5  4x - 4 + 2 - 3x
4x - 4 + 2 - 3x  5
5  -(4x-4+2-3x)
-(4x-4+2-3x) 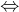 5
5  x-2
x-2  5
5  -x + 2
-x + 2 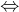 7
7 x
x  x
x  3
3
a to nie je spravny vysledok
Offline
