Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Báze obrazu zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 11. 2018 12:15
Báze obrazu zobrazení
Ahoj,
nejsem si jistá, jak mám dopočítat bázi obrazu zobrazení. Vyberu lineárně nezávislé vektory, ale jsou to ty, co mi vyjdou v matici v schodovitém tvaru, nebo tam mám dát ty z původních polynomů?
Na fotce mám postup, jak jsem řešila a obě možnosti dole zakroužkované. Zadání je spočítat bázi obrazu a jádra zobrazení psí.
Moc děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) 4d4nsoni4)
#2 22. 11. 2018 09:18
Re: Báze obrazu zobrazení
Nejdříve si musíme uvědomit, že obraz zobrazení 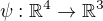 je podprostorem prostoru
je podprostorem prostoru 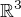 a jádro tohoto zobrazení je podprostorem prostoru
a jádro tohoto zobrazení je podprostorem prostoru 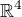 .
.
Původní matice, kterou tam máš, popisuje dané zobrazení vůči standardním bázím prostorů 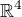 a
a 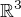 . Ve sloupcích matice zobrazení jsou souřadnice (vůči standardní bázi prostoru
. Ve sloupcích matice zobrazení jsou souřadnice (vůči standardní bázi prostoru 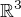 ) obrazů vektorů standardní báze prostoru
) obrazů vektorů standardní báze prostoru 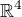 . Z těchto 4 sloupců potřebujeme vybrat lineárně nezávislý soubor sloupců, abychom našli bázi obrazu zobrazení. Takže je třeba dělat v matici sloupcové (ne řádkové) ekvivalentní úpravy, abychom matici upravili do stupňovitého tvaru a mohli vybrat lineárně nezávislý soubor sloupců.
. Z těchto 4 sloupců potřebujeme vybrat lineárně nezávislý soubor sloupců, abychom našli bázi obrazu zobrazení. Takže je třeba dělat v matici sloupcové (ne řádkové) ekvivalentní úpravy, abychom matici upravili do stupňovitého tvaru a mohli vybrat lineárně nezávislý soubor sloupců.
Pro nalezení báze jádra zobrazení 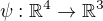 definovaného maticí
definovaného maticí  řešíme rovnici
řešíme rovnici 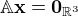 . Tentokrát už děláme ekvivalentní řádkové úpravy. Je to soustava 3 rovnic se 4 neznámými, takže alespoň jednu neznámou můžeme volit libovolně (například
. Tentokrát už děláme ekvivalentní řádkové úpravy. Je to soustava 3 rovnic se 4 neznámými, takže alespoň jednu neznámou můžeme volit libovolně (například 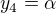 ), takže najdeme řešení
), takže najdeme řešení  ve tvaru nějaké lineární kombinace vektorů, minimálně ve tvaru
ve tvaru nějaké lineární kombinace vektorů, minimálně ve tvaru  -násobku nějakého nenulového vektoru. Z těchto vektorů vybereme lineárně nezávislý soubor vektorů a máme bázi jádra zobrazení.
-násobku nějakého nenulového vektoru. Z těchto vektorů vybereme lineárně nezávislý soubor vektorů a máme bázi jádra zobrazení.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Báze obrazu zobrazení (TOTO TÉMA JE VYŘEŠENÉ)