Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 26. 11. 2018 21:37
Re: Stejnoměrná konvergence
↑ Pomeranc: Ide o obycajnu konvergenciu postupnosti funkcii v priestore funkcii so supremovou metrikou.
Offline
#3 26. 11. 2018 21:47
Re: Stejnoměrná konvergence
↑ Pomeranc:
Nedávno se tu 2x řešila funkce, která stejnoměrně konvergentní není - zkus si to najít. Pak asi pochopíš, v čem to spočívá.
Laicky řečeno - když funkce konverguje stejnoměrně, musí konvergovat "shora", pokud né, může konvergovat "zboku" - tj že obsahuje nějaký "hrb", který se nezmenšuje, ale zužuje. Takže v každém bodě to sice konverguje, ale pořád existuje nějaké místo (nějaký bod), kde se to od výsledné funkce hodně liší.
Online
#4 26. 11. 2018 22:00
Re: Stejnoměrná konvergence
↑ MichalAld: Upresnim, ze ide nie o konvergenciu funkcie, ale postupnosti funkcii. Zadavatel sa s tymto pojmom zrejme iba zoznamuje, tak nech ma v terminologii jasno.
Offline
#5 26. 11. 2018 22:05
Re: Stejnoměrná konvergence
↑ Pomeranc:
Ahoj.
Nejprve si vysledujes bodovou konvergenci,t.j. volis jednotliva x a posles n do nekonecna,tak dostanes funkci f(x).Pri stejnomerne konvergenci si zvolis pas sire epsilon,pocinaje nejakym n indexem funkce v zavislosti na epsilon musi byt vzdalenost fn(x) ;f(x) mensi nez epsilon.,a to pro vsechna x z uvazovane mnoziny.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#6 26. 11. 2018 22:48
#7 26. 11. 2018 22:53 — Editoval MichalAld (26. 11. 2018 22:54)
Re: Stejnoměrná konvergence
Příklad posloupnosti funkcí, která nekonverguje stejnoměrně je třeba tato: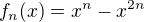
a řeší se konvergence na intervalu <0; 1>
bodově to konverguje k funkci f(x) = 0. Ale pro každé n bude mít ta funkce někde na uvedeném intervalu takový hrb, a ten je stále stejně vysoký - jen se posouvá a zužuje.
A tady je graf několika vybraných funkcí z posloupnosti (myší to lze zvětšovat).
Online
#8 26. 11. 2018 23:01
Re: Stejnoměrná konvergence
Asi najjednoduchšie je povedať, že v prípade rovnomernej konvergencie číslo delta ktoré má ku kladnému epsilon podľa definície existovať závisí len na epsilon (je univerzálne pre všetky x), zatiaľ čo pri bodovej konvergencii môže závisieť aj na danom x.
MATH IS THE BEST!!!
Offline
#9 26. 11. 2018 23:54
Re: Stejnoměrná konvergence
↑ MichalAld:
Stačí vzít posloupnost funkcí 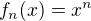 , na intervalu
, na intervalu  , která bodově konverguje k funkci
, která bodově konverguje k funkci 
stejnoměrně však nikoliv.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 29. 11. 2018 19:08
Re: Stejnoměrná konvergence
Děkuji všem za odpovědi a omlouvám se za zpoždění.
Ta bodová konvergence dává smysl. Mám posloupnost funkcí zafixuju si každé x a n pošlu do nekonečna.
Resp. to lze i říct, že pro každé x existuje nějaká limita.
U té stejnoměrné konvergence úplně nevím, co mi to říká, když to pro každé x je přesunuté oproti def bodové konvergence. Slyšela jsem i formulaci typu, že to znamená, že pro všechna x to konverguje stejnou rychlostí.
Celkově jsem zjistila, že když je kopeček, který se nezmenšuje, ale jenom se přesouvá, tak to nestejnoměrně konverguje.
Offline
#12 29. 11. 2018 21:23
Re: Stejnoměrná konvergence
Pomeranc napsal(a):
Celkově jsem zjistila, že když je kopeček, který se nezmenšuje, ale jenom se přesouvá, tak to nestejnoměrně konverguje.
Nevím, jestli se může říkat "nestejnoměrně konverguje", správně je to "nekonverguje stejnoměrně".
Jinak je to pravda - ale je to taková laická představa.
Správná představa je asi tahle....ale nejprve je nutné si udělat správnou představu o tom, co to vůbec znamená "konverguje". Znamená to, že když si zvolíme nějakou malinkou odchylku od té výsledné hodnoty v bodě x, tak se nám vždy podaří najít takové n, že máme skutečnou odchylku menší než tu, co jsme si zvolili. S tímhle je třeba se srovnat.
Pak už je to snadné, stejnoměrně to konverguje, když si zvolíme tu malinkou odchylku, a volbou dostatečně velkého n máme skutečnou odchylku menší VE VŠECH BODECH (né jen v jednom konkrétním).
Samozřejmě to musí být tak, aby nezáleželo na tom, jak malou si tu požadovanou odchylku zvolíme.
Takže když si řeknu, že |f(x) - fn(x)| musí být menší než třeba 0.000001, tak musí existovat n, pro které je to pravda. Bodově to konverguje tehdy, když pro každý bod x dokážu takové n najít. Stejnoměrně to konverguje tehdy, když takové n dokážu najít aby to platilo pro všechna x najednou.
A tady je právě vidět, proč ty posloupnosti, které konvergují "zboku" - tj že se kopeček zužuje a uhýbá, ale nesnižuje, že ty stejnoměrně nekonvergují. Protože pro každé zvolené n ten kopeček někde bude - a tam tu velmi malou odchylku nezískáme.
Online
#13 29. 11. 2018 23:25 — Editoval krakonoš (30. 11. 2018 01:45)
Re: Stejnoměrná konvergence
↑ MichalAld:
Ahoj.
Nutno poznamenat,ze snižování kopečků u zadané posloupnosti funkcí platí při konvergenci k nulové funkci f(x).
Funkce f(x) ale vůbec někdy nemusí být nulová. Vezmeme-li hustoty normálního rozdělení o nulové střední hodnotě a zvyšujeme rozptyly jako n.Bude f(x) rovna 1.Stejnoměrná konvergence zkrachuje pro x v nekonečnu,tam to jde k nule,zatimco f(x) je 1,a nebude to na R stejnoměrně konvergovat.
My vlastně zkoumáme největší absolutní hodnoty fn(x)-f(x) a ty s rostoucím n musí jít k nule.
Ale říkám si,jak se to projeví v tom počítačovém programu ,když to krachuje v nekonečnu??
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#14 30. 11. 2018 12:10
Re: Stejnoměrná konvergence
↑ krakonoš:
1) Podle mě je mnohem zajímavější analyzovat, k čemu konverguje posloupnost hustot normálního rozdělení když se sigma blíží k nule...a přitom zůstává jednotková plocha.
Online
#15 30. 11. 2018 14:10
Re: Stejnoměrná konvergence
↑ MichalAld:
No,tam to uz vubec nefunguje.f(x) je jednobodova,nespojita,a tak nemuze jit o stejnomernou konvergenci uz vubec.Zuzovanim zvonu se to cele zhrouti,si predstavuji ja.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline

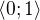 nekonverguje stejnoměrně, na intervalu
nekonverguje stejnoměrně, na intervalu 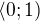 také ne, ale pro každé
také ne, ale pro každé 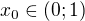 (i libovolně blízké k jedničce) stejnoměrně konverguje na intervalu
(i libovolně blízké k jedničce) stejnoměrně konverguje na intervalu 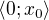 .
.